by Patrick Lynch
01 May 2004
In the article on portfolio theory, we saw that the motivation behind the establishment of a portfolio is that risk (the bad) can be reduced without a consequential reduction in return (the good). This was mathematically evident when the portfolios' expected return was equal to the weighted average of the expected returns on the individual investments, while the portfolio risk was normally less than the weighted average of the risk of the individual investments.
The portfolio's total risk (as measured by the standard deviation of returns) consists of unsystematic and systematic risk. We saw the dramatic risk reduction effect of diversification (see Example 1). If an investor invests in just 15 companies in different sectors (a well-diversified portfolio), it is possible to virtually eliminate unsystematic risk. The only risk affecting a well-diversified portfolio is therefore systematic. As a result, an investor who holds a well-diversified portfolio will only require a return for systematic risk. In this article, we explain how to measure an investment's systematic risk.
Learning Objectives
By the end of this article you should be able to:
- calculate beta from basic data using two different formulae
- calculate the required return using the CAPM formula
- understand the meaning of beta
- prepare an alpha table and understand the nature of the alpha value
- explain the problems with CAPM
- briefly explain the arbitrage pricing model (APM)
- calculate the portfolio risk of a multi-asset portfolio when there is no correlation between the return of the investments.
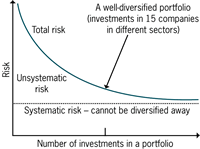
The measurement of systematic risk
You may recall from the previous article on portfolio theory that the formula of the variance of a large portfolio (where we invest equal amounts in each investment) is:

The first term is the average variance of the individual investments (unsystematic risk). As N becomes very large, the first term tends towards zero. Thus, unsystematic risk can be diversified away.
The second term is the covariance term and it measures systematic risk. As N becomes large, the second term will approach the average covariance. The risk contributed by the covariance (the systematic risk) cannot be diversified away.
Systematic risk reflects market-wide factors such as the country's rate of economic growth, corporate tax rates, interest rates etc. Since these market-wide factors generally cause returns to move in the same direction they cannot cancel out.
Therefore, systematic risk remains present in all portfolios. Some investments will be more sensitive to market factors than others and will therefore have a higher systematic risk.
Remember that investors who hold well-diversified portfolios will find that the risk affecting the portfolio is wholly systematic. Unsystematic risk has been diversified away. These investors may want to measure the systematic risk of each individual investment within their portfolio, or of a potential new investment to be added to the portfolio. A single investment is affected by both systematic and unsystematic risk but if an investor owns a well-diversified portfolio then only the systematic risk of that investment would be relevant. If a single investment becomes part of a well-diversified portfolio the unsystematic risk can be ignored.
The systematic risk of an investment is measured by the covariance of an investment's return with the returns of the market. Once the systematic risk of an investment is calculated, it is then divided by the market risk, to calculate a relative measure of systematic risk. This relative measure of risk is called the ‘beta' and is usually represented by the symbol b. If an investment has twice as much systematic risk as the market, it would have a beta of two. There are two different formulae for beta. The first is:

You must commit both formulae to memory, as they are not given on the exam formulae sheet. The formula that you need to use in the exam will be determined by the information given in the question. If you are given the covariance, use the first formula or if you are given the correlation coefficient, use the second formula.
Example 2
You are considering investing in Y plc. The covariance between the company's returns and the return on the market is 30%. The standard deviation of the returns on the market is 5%.
Calculate the beta value:
be =
30% = 1.2
52%
Example 3
You are considering investing in Z plc. The correlation coefficient between the company's returns and the return on the market is 0.7. The standard deviation of the returns for the company and the market are 8% and 5% respectively.
Calculate the beta value:
be =
0.7 x 8% = 1.12
5%
Investors make investment decisions about the future. Therefore, it is necessary to calculate the future beta. Obviously, the future cannot be foreseen. As a result, it is difficult to obtain an estimate of the likely future co-movements of the returns on a share and the market. However, in the real world the most popular method is to observe the historical relationships between the returns and then assume that this covariance will continue into the future. You will not be required to calculate the beta value using this approach in the exam.
The CAPM Formula
The capital asset pricing model (CAPM) provides the required return based on the perceived level of systematic risk of an investment:

The calculation of the required return
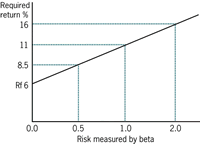
The required return on a share will depend on the systematic risk of the share. What is the required return on the following shares if the return on the market is 11% and the risk free rate is 6%?
The shares in B plc have a beta value of 0.5
Answer: 6% + (11% - 6%) 0.5 = 8.5%
The shares in C plc have a beta value of 1.0
Answer: 6% + (11% - 6%) 1.0 = 11%
The shares in D plc have a beta value of 2.0
Answer: 6% + (11% - 6%) 2.0 = 16%.
Obviously, with hindsight there was no need to calculate the required return for C plc as it has a beta of one and therefore the same level of risk as the market and will require the same level of return as the market, ie the RM of 11%. The systematic risk-return relationship is graphically demonstrated by the security market line. See Example 4.
Example 4
The CAPM contends that the systematic risk-return relationship is positive (the higher the risk the higher the return) and linear.
If we use our common sense, we probably agree that the risk-return relationship should be positive. However, it is hard to accept that in our complex and dynamic world that the relationship will neatly conform to a linear pattern. Indeed, there have been doubts raised about the accuracy of the CAPM.
The meaning of beta
The CAPM contends that shares co-move with the market. If the market moves by 1% and a share has a beta of two, then the return on the share would move by 2%. The beta indicates the sensitivity of the return on shares with the return on the market. Some companies' activities are more sensitive to changes in the market - eg luxury car manufacturers - have high betas, while those relating to goods and services likely to be in demand irrespective of the economic cycle - eg food manufacturers - have lower betas. The beta value of 1.0 is the benchmark against which all share betas are measured.
- Beta > 1 - aggressive shares
These shares tend to go up faster then the market in a rising(bull) market and fall more than the market in a declining (bear) market. - Beta < 1 - defensive shares
These shares will generally experience smaller than average gains in a rising market and smaller than average falls in a declining market. - Beta = 1 - neutral shares
These shares are expected to follow the market.
The beta value of a share is normally between 0 and 2.5. A risk-free investment (a treasury bill) has a b = 0 (no risk). The most risky shares like some of the more questionable penny share investments would have a beta value closer to 2.5. Therefore, if you are in the exam and you calculate a beta of 11 you know that you have made a mistake.
Basic exam application of CAPM
1. Capital investment decisions
The calculation of Ke in the WACC calculation to enable an NPV calculation
A shareholder's required return on a project will depend on the project's perceived level of systematic risk. Different projects generally have different levels of systematic risk and therefore shareholders have a different required return for each project. A shareholder's required return is the minimum return the company must earn on the project in order to compensate the shareholder. It therefore becomes the company's cost of equity.
Example 5
E plc is evaluating a project which has a beta value of 1.5. The return on the FTSE All-Share Index is 15%. The return on treasury bills is 5%.
Required:
What is the cost of equity?
Answer:
5% + (15% - 5%) 1.5 = 20%
2. Stock market investment decisions
When we read the financial section of newspapers, it is commonplace to see analysts advising us that it is a good time to buy, sell, or hold certain shares. The CAPM is one method that may employed by analysts to help them reach their conclusions. An analyst would calculate the expected return and required return for each share. They then subtract the required return from the expected return for each share, ie they calculate the alpha value (or abnormal return) for each share. They would then construct an alpha table to present their findings.
Example 6
We are considering investing in F plc or G plc. Their beta values and expected returns are as follows:
Beta values Expected returns
F plc 1.5 18%
G plc 1.1 18%
The market return is 15% and the risk-free return is 5%.
Required:
What investment advice would you give us?
Answer:
Alpha table
Expected returns Required returns Alpha values F plc 18% 5% + (15% - 5%) -2%
1.5 = 20%
G plc 18% 5% + (15% - 5%) +2%
1.1 = 16%
Sell shares in F plc as the expected return does not compensate the investors for its perceived level of systematic risk, it has a negative alpha. Buy shares in G plc as the expected return more than compensates the investors for its perceived level of systematic risk, ie it has a positive alpha.
3. The preparation of an alpha table for a portfolio
The portfolio beta is a weighted average
A common exam-style question is a combined portfolio theory and CAPM question. A good example of this is the Oriel plc question at the end of this article where you are asked to calculate the alpha table for a portfolio.
The expected return of the portfolio is calculated as normal (a weighted average) and goes in the first column in the alpha table. We then have to calculate the required return of the portfolio. To do this we must first calculate the portfolio beta, which is the weighted average of the individual betas. Then we can calculate the required return of the portfolio using the CAPM formula.
Example 7
The expected return of the portfolio A + B is 20%. The return on the market is 15% and the risk-free rate is 6%. 80% of your funds are invested in A plc and the balance is invested in B plc. The beta of A is 1.6 and the beta of B is 1.1.
Required:
Prepare the alpha table for the Portfolio
(A + B)
Answer:
b(A + B) = (1.6 × .80) + (1.1 × .20)
= 1.5
R portfolio (A + B) = 6% + (15% - 6%) 1.5 = 19.50%
Alpha table
Expected return Required return Alpha value
Portfolio (A + B) 20% 19.50% 0.50%
The Alpha Value
If the CAPM is a realistic model (that is, it correctly reflects the risk-return relationship) and the stock market is efficient (at least weak and semi-strong), then the alpha values reflect a temporary abnormal return. In an efficient market, the expected and required returns are equal, ie a zero alpha. Investors are exactly compensated for the level of perceived systematic risk in an investment, ie shares are fairly priced. Arbitrage profit taking would ensure that any existing alpha values would be on a journey towards zero.
Remember in Example 6 that the shares in G plc had a positive alpha of 2%. This would encourage investors to buy these shares. As a result of the increased demand, the current share price would increase (which if you recall from the portfolio theory article is the denominator in the expected return calculation) thus the expected return would fall. The expected return would keep falling until it reaches 16%, the level of the required return and the alpha becomes zero.
The opposite is true for shares with a negative alpha. This would encourage investors to sell these shares. As a result of the increased supply, the current share price would decrease thus the expected return would increase until it reaches the level of the required return and the alpha value becomes zero.
It is worth noting that when the share price changes, the expected return changes and thus the alpha value changes. Therefore, we can say that alpha values are as dynamic as the share price. Of course, alpha values may exist because CAPM does not perfectly capture the risk-return relationship due to the various problems with the model.
Problems with CAPM
Investors hold well-diversified portfolios
CAPM assumes that all the company's shareholders hold well-diversified portfolios and therefore need only consider systematic risk. However, a considerable number of private investors in the UK do not hold well-diversified portfolios.
One period model
CAPM is a one period model, while most investment projects tend to be over a number of years.
Assumes the stock market is a perfect capital market
This is based on the following unrealistic assumptions:
- no individual dominates the market
- all investors are rational and risk-averse
- investors have perfect information
- all investors can borrow or lend at the risk-free rate
- no transaction costs.
Evidence
CAPM does not correctly express the risk-return relationship in some circumstances. To cite a number of these circumstances they are, for small companies, high and low beta companies, low PE companies, and certain days of the week or months of the year.
Estimation of future b based on past b
A scatter diagram is prepared of the share's historical risk premium plotted against the historical market risk premium usually over the last five years. The slope of the resulting line of best fit will be the b value. The difficulty of using historic data is that it assumes that historic relationships will continue into the future. This is questionable, as betas tend to be unstable over time.
Data input problems
Richard Roll (1977) criticised CAPM as untestable, because the FTSE All-Share Index is a poor substitute for the true market, ie all the risky investments worldwide. How can the risk and return of the market be established as a whole? What is the appropriate risk-free rate? However, despite the problems with CAPM, it provides a simple and reasonably accurate way of expressing the risk-return relationship. Quite simply, CAPM is not perfect but it is the best model that we have at the moment.
Additionally, some critics believe that the relationship between risk and return is more complex than the simple linear relationship defined by CAPM. Another model may possibly replace CAPM in the future. The most likely potential successor to CAPM is the arbitrage pricing model (APM).
The Arbitrage Pricing Model - APM
The CAPM contends that the only reason the return of a share moves is because the return on the market moves. The magnitude of a share's co-movement with the market is measured by its beta. If a share has a beta of two and the market increases by 1%, we would expect the share's return to increase by 2%. If the market increases by 5% we would expect the share's return to increase by 10%. Remember that the market only gives a return for systematic risk. Therefore, any changes in the market return are due to a large number of macro-economic factors.
The model
The arbitrage pricing model, developed by Stephen Ross in 1976, attempts to identify all of the macro-economic factors and then specifies how each factor would affect the return of a particular share. The APM is therefore more sophisticated than CAPM in that it attempts to identify the specific macro-economic factors that influence the return of a particular share. Commonly invoked factors are:
- inflation
- industrial production
- market risk premiums
- interest rates
- oil prices.
Each share will have a different set of factors and a different degree of sensitivity (beta) to each of the factors. To construct the APM for a share we require the risk premiums and the betas for each of the relevant factors.
Return on a share = RF + Risk premium F1.b1 + Risk premium F2.b2 + Risk premium F3.b3 + . . .
Example 8
beta 1 = the effect of changes in interest rates on the returns from a share
beta 2 = the effect of oil prices on the returns from a share
A share in a retail furniture company may have a high beta 1 and a low beta 2 whereas a share in a haulage company may have a low beta 1 and a high beta 2. Under the APM, these differences can be taken into account. However, despite its theoretical merits, APM scores poorly on practical application. The main problem is that it is extremely difficult to identify the relevant individual factors and the appropriate sensitivities of such factors for an individual share. This has meant that APM has not been widely adopted in the investment community as a practical decision-making tool despite its intuitive appeal.
Before we conclude the articles on the risk-return relationship, it is essential that we see the practical application of both portfolio theory and CAPM in an exam-style question. Indeed, it is quite common to have both topics examined in the same question as demonstrated in Oriel plc below.
Exam Style Question (including the multi-asset portfolio exam trick)
Oriel plc
Oriel plc is considering investing in one of two short-term portfolios of four short-term financial investments. The correlation between the returns of the individual investments is believed to be negligible (zero/independent/no correlation). See Portfolio 1 and Portfolio 2. The market return is estimated to be 15%, and the risk free rate 5%
| Portfolio 1 | ||||
| Investment | Amounts invested £ million | Expected return | Total risk | Beta |
| a | 10 | 20% | 8 | 0.7 |
| b | 40 | 22% | 10 | 1.2 |
| c | 30 | 24% | 11 | 1.3 |
| d | 20 | 26% | 9 | 1.4 |
| Portfolio 2 | ||||
| Investment | Amounts invested £ million | Expected return | Total risk | Beta |
| a | 20 | 18% | 7 | 0.8 |
| b | 40 | 20% | 9 | 1.1 |
| c | 20 | 22% | 12 | 1.2 |
| d | 20 | 16% | 13 | 1.4 |
Required:
Estimate the risk and return of the two portfolios using the principles of both portfolio theory and CAPM and decide which one should be selected.
How would you alter your calculations for the summary table if you were told: ‘The correlation between the returns of the individual investments is perfectly positively correlated'.
Solution to Oriel plc
Answer to part (a)
The CAPM calculations - the application of CAPM principles in the exam means the preparation of the alpha table to find the portfolio with the largest positive alpha. See Portfolio 1 Solution and Portfolio 2 Solution.
| Portfilio 1 Solution | |||||
| Investment | Investment weightings | Expected return (%) | Portfolio expected return (%) | Beta | Portfolio beta |
| a | .1 | 20 | 2.00 | 0.7 | .07 |
| b | .4 | 22 | 8.80 | 1.2 | .48 |
| c | .3 | 24 | 7.20 | 1.3 | .39 |
| d | .2 | 26 | 5.20 | 1.4 | .28 |
| 23.20 | 1.22 | ||||
| The required return: 5 + (15 - 5) 1.12=16.20% | |||||
| Portfolio 2 Solution | |||||
| Investment | Investment weightings | Expected return (%) | Portfolio expected return (%) | Beta | Portfolio beta |
| a | .2 | 18 | 3.60 | 0.8 | .16 |
| b | .4 | 20 | 8.00 | 1.1 | .44 |
| c | .2 | 22 | 4.40 | 1.2 | .24 |
| d | .2 | 16 | 3.20 | 1.4 | .28 |
| 19.20 | 1.12 | ||||
| The required return: 5 + (15 - 5) 1.12 = 16.20% |
Alpha table
Expected returns Required returns Alpha values
Portfolio 1 23.20% 17.20% 6.00%
Portfolio 2 19.20% 16.20% 3.00%
Portfolio 1 is chosen because it has the largest positive alpha.
Portfolio theory calculations
The application of the portfolio theory principles in the exam requires the preparation of a summary table to help identify the efficient portfolio. However, in this question we are dealing with more than a two-asset portfolio, in fact there are four assets in each portfolio. This is known as the multi-asset portfolio exam trick. This was examined in Rodfin (December 1995) and Maltec (June 2001). Both times you were told there is no correlation between the returns of the individual investments. Therefore, the correlation coefficient is zero and the third term disappears from the portfolio risk equation.
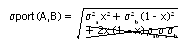
Therefore, the formula for a multi-asset portfolio with no correlation between the returns is:
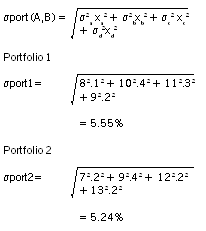
Summary table
Expected returns Portfolio risk
Portfolio 1 23.20% 5.55%
Portfolio 2 19.20% 5.24%
The portfolio with the highest return also has the highest level of risk. Therefore, neither portfolio can be said to be more efficient than the other. An objective answer cannot be reached. As the company is making decisions on behalf of its shareholders the correct way to evaluate the investments is by looking at the effect they have on a shareholders existing/enlarged portfolios.
Thus, the portfolio theory decision rule will probably break down if different shareholders experience different levels of total risk or they may have different attitudes to risk. Therefore, some shareholders would prefer portfolio 1 and other shareholders portfolio 2.
If the majority of Oriel's shareholders are institutional shareholders, I would recommend the use of CAPM to make the decision, as they would hold well-diversified portfolios and only be subject to systematic risk. This would be a reasonable assumption as institutional investors like pension companies and unit trust companies hold approximately 75% of all the shares that are quoted on the London stock market.
Answer to part (b)
If the correlation coefficient identifies perfect positive correlation, there is no reduction in risk at all. Therefore, the portfolio's total risk is simply a weighted average of the total risk (as measured by the standard deviation) of the individual investments of the portfolio.
sport1 = 8 × 0.1 + 10 × 0.4 + 11 × 0.3 + 9 × 0.2 = 9.9
sport2 = 7 × 0.2 + 9 × 0.4 + 12 × 0.2 + 13 × 0.2 = 10
Summary table
Expected returns Portfolio risk
Portfolio 1 23.20% 9.9%
Portfolio 2 19.20% 10.0%
Portfolio 1 is the most efficient portfolio as it gives us the highest return for the lowest level of risk.
10 Key Points To Remember
1. The beta is a relative measure of systematic risk. It indicates the sensitivity of the return on a share with the return on the market. If the market moves by 1% and a share has a beta of two, then the return on the share would move by 2%.
2. We may have to calculate the beta from basic data using the following two different formulae:
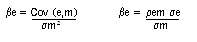
3. The value of beta is normally between 0 and 2.5.
4. Ensure that you know how to calculate the required return using the CAPM formula:
RA = RF + (RM - RF) bA
as this is examined in every paper.
5. Be able to prepare an alpha table and to give investment advice based on alpha values:
Decision advice based on alpha values
Alpha Have shares Don’t have shares
+ Hold Buy
- Sell Don’t buy
6. If CAPM is a realistic model and the market is efficient, an alpha value (a temporary abnormal return) is on a journey towards zero.
7. Ensure that you are able to list the problems associated with CAPM.
8. APM suggests that a number of factors affect the risk-return relationship and in time, this model may replace CAPM when more developments take place to improve its practical application.
9. Remember that the formula for a multi-asset portfolio with no correlation between the returns is:
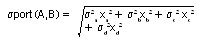
10. The basic exam technique required for portfolio theory is the preparation of a summary table to aid identification of the most efficient portfolio. Similarly, the key to applying CAPM is the preparation of an alpha table to help identify the largest positive alpha value.
Patrick Lynch is a lecturer at FTC London


