Способность понять взаимосвязь между различными факторами очень важна для организаций. Например, было бы полезно понять взаимосвязь между расходами на рекламу и продажами, полученными в результате этих расходов на рекламу, или между уровнем производства и общими затратами на производство. Понимание этих взаимосвязей позволяет организациям лучше прогнозировать, какими будут продажи или затраты в будущем. Это будет иметь неоценимое значение при составлении бюджета или прогнозировании.
В данной статье будет рассмотрено, как отношения между переменными могут быть проанализированы с использованием метода «линии наилучшего соответствия» и регрессионного анализа, а также как сила этих отношений может быть измерена с помощью корреляции.
Взаимосвязь между переменными
В любом отношении между двумя переменными есть независимая переменная и зависимая переменная, причем степень изменения зависимой переменной зависит от степени изменения независимой переменной. Например; общая себестоимость производственного процесса будет зависеть от уровня деятельности.
Рассмотрим следующие данные, полученные компанией за последние два года.
| Уровень (000 единиц) |
Общие производственные затраты ($000) |
|
| 20X1 Q1 | 15 | 300 |
| 20X1 Q2 | 45 | 615 |
| 20X1 Q3 | 25 | 470 |
| 20X1 Q4 | 55 | 680 |
| 20X2 Q1 | 30 | 520 |
| 20X2 Q2 | 20 | 350 |
| 20X2 Q3 | 35 | 590 |
| 20X2 Q4 | 60 | 740 |
Компания хочет понять взаимосвязь между уровнем активности и общими производственными затратами, чтобы иметь возможность прогнозировать общие производственные затраты в будущем.
Линия наилучшего соответствия
Одним из методов понимания взаимосвязи между переменными является метод линии наилучшего соответствия. Все приведенные данные нанесены на график. Уровень активности является независимой переменной (как описано выше) и показан на оси x (горизонтальной). Общие производственные затраты являются зависимой переменной и показаны на оси Y (вертикальной).
После того, как все данные нанесены на график, можно провести линию наилучшего соответствия:
В этом случае некоторые точки находятся на линии, а некоторые выше и ниже, но большинство из них находятся близко к линии, что предполагает наличие связи между уровнем активности и общими производственными затратами.
Эту «линию наилучшего соответствия» можно использовать для прогнозирования того, что произойдет на других уровнях производства. Для уровней производства, которые не попадают в диапазон предыдущих уровней, можно экстраполировать «линию наилучшего соответствия» для прогнозирования других уровней, считывая значения с диаграммы.
Это простая техника, но она имеет некоторые ограничения. Основным из них является то, что «линия наилучшего соответствия» определяется по нанесенным точкам данных, и через один и тот же набор точек могут быть проведены разные линии. Методом, который может преодолеть этот недостаток, является регрессионный анализ.
Регрессионный анализ
Регрессионный анализ также использует исторические данные и находит линию наилучшего соответствия, но применяет статистический подход, что делает результирующую линию более надежной.
Мы предполагаем линейную (прямолинейную) связь между переменными и что уравнение прямой линии имеет вид:
y = a + bx
где:
a — фиксированный элемент (где линия пересекает ось y)
b — переменный элемент (градиент линии) и
x и y относятся к переменным x и y.
a и b рассчитываются по следующим формулам:
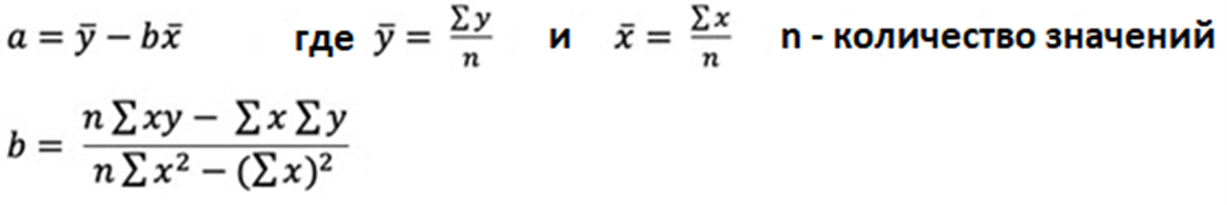
Эти формулы приведены на листе формул PM.
Самый простой способ выполнить эти расчеты — сначала создать таблицу со столбцами для x, y, xy и x2.
Примечание: в таблице также есть столбец для y2. Он потребуется для последующих расчетов
| Единицы (000s) x |
Общие затраты ($000) y |
xy |
x2 |
y2 |
|
| 20X1 Q1 | 15 | 300 | 4,500 | 225 | 90,000 |
| 20X1 Q2 | 45 | 615 | 27,675 | 2,025 | 378,225 |
| 20X1 Q3 | 25 | 470 | 11,750 | 625 | 220,900 |
| 20X1 Q4 | 55 | 680 | 37,400 | 3,025 | 462,400 |
| 20X2 Q1 | 30 | 520 | 15,600 | 900 | 270,400 |
| 20X2 Q2 | 20 | 350 | 7,000 | 400 | 122,500 |
| 20X2 Q3 | 35 | 590 | 20,650 | 1,225 | 348,100 |
| 20X2 Q4 | 60 | 740 | 44,400 | 3,600 | 547,600 |
| Totals (∑) | 285 | 4,265 | 168,975 | 12,025 | 2,440,125 |
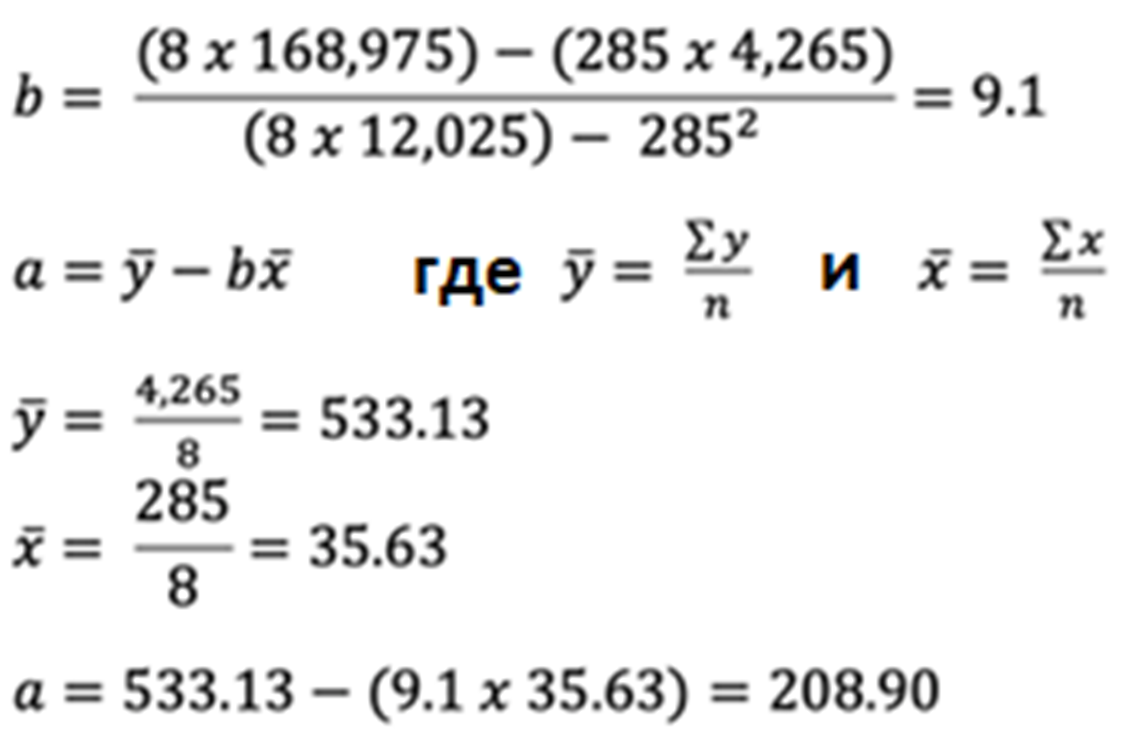
Уравнение линии регрессии (в форме y = a + bx) принимает вид:
y = 208.90 + 9.1x
Используя это уравнение, легко спрогнозировать общие затраты на разных уровнях производства, например, для уровня производства 80 000 единиц оценка общих затрат будет:
208.90 + (9.1 x 80) = 936.90, или $936,900.
Насколько надежна эта оценка, будет зависеть от силы связи между двумя переменными; в какой степени изменение у можно объяснить изменением х?
Чем сильнее связь между переменными, тем больше можно полагаться на рассчитанное уравнение и тем лучше будут прогнозы.
Мерой силы связи между переменными является корреляция.
Корреляция
Считается, что две переменные коррелируют, если они связаны друг с другом и если изменения одной из них сопровождаются изменениями другой. Корреляция может быть положительной (когда увеличение одной переменной приводит к увеличению другой) или отрицательной (когда увеличение одной переменной приводит к уменьшению другой).
Диаграмма, показанная в разделе «линия наилучшего соответствия» выше, показывает сильную положительную корреляцию. Некоторые другие отношения показаны ниже:
Возможно, что корреляции между переменными нет. Горизонтальная линия предполагает отсутствие корреляции, как в следующем примере:
Если компания хочет использовать прошлые данные для прогнозирования будущего, чем сильнее корреляция, тем точнее будут оценки.
Силу корреляции между переменными можно измерить с помощью коэффициента корреляции, который можно рассчитать по следующей формуле:

r = 1 обозначает идеальную положительную линейную корреляцию
r = -1 обозначает идеальную отрицательную линейную корреляцию
r = 0 означает отсутствие линейной корреляции
Значение коэффициента корреляции должно находиться в диапазоне от -1 до 1. Чем ближе значение к 1 и -1, тем сильнее корреляция.
Используя предыдущий пример для вычисления r:
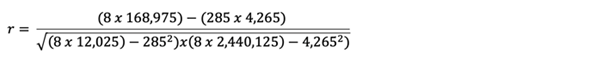
Дальнейшим расчетом является коэффициент детерминации, который рассчитывается как r2.
Коэффициент детерминации определяет долю изменений у (зависимой переменной), которую можно объяснить изменениями х (независимая переменная). В этом примере r2 = 0,931, поэтому 93,1% изменений общих производственных затрат можно объяснить изменениями уровня активности. Это означает, что 6,9% изменений должны быть связаны с другими факторами.
Заключение
Следует соблюдать осторожность при использовании регрессионного анализа и корреляции для прогнозов на будущее. Проведенные расчеты могут только предположить наличие связи между факторами, но не могут ее доказать. Возможно, есть и другие факторы, влияющие на изменения переменных, которые не учитывались.
Кроме того, как и анализ временных рядов, который рассматривается в отдельной статье, регрессионный анализ использует прошлые наблюдения, чтобы попытаться предсказать, что произойдет в будущем. Предположение, что то, что произошло в прошлом, является хорошим индикатором того, что произойдет в будущем, является упрощенным предположением. В реальном мире изменения в окружающей среде (технологические, социальные, экологические, политические, экономические и т. д.) могут создавать неопределенность, делая прогнозы, основанные на данных о прошлом, нереалистичными.
Написано членом экзаменационной группы по Управлению эффективностью


