Decision making is an important aspect of the Performance Management syllabus, and questions on this topic will be common. The range of possible questions is considerable, but this article will focus on only one: linear programming
The ideas presented in this article are based on a simple example. Suppose a profit-seeking firm has two constraints: labour, limited to 16,000 hours, and materials, limited to 15,000kg. The firm manufactures and sells two products, X and Y. To make X, the firm uses three kgs of material and four hours of labour, whereas to make Y, the firm uses five kgs of material and four hours of labour. The contribution per unit made by each product are $30 for X and $40 for Y. The cost of materials is normally $8 per kg, and the labour rate is $10 per hour.
The first step in any linear programming problem is to define the variables and the objective function. Defining the variables simply means stating what letter you are going to use to represent the products in the subsequent equations as follows;
Let X = number of X to be produced
Let Y = number of Y to be produced
The objective function is essentially the contribution formula as the objective is to maximise contribution and therefore profit.
Contribution = ($30 x units of X produced) + ($40 x units of Y produced), therefore:
C = 30X + 40Y
The next step is to define the constraints. In our example, the materials constraint will be 3X + 5Y ≤ 15,000, and the labour constraint will be 4X + 4Y ≤ 16,000.
Note: You should not forget the non-negativity constraint, if needed, of X,Y ≥ 0.
In order to plot the graph you need to solve the constraints. This gives us the co-ordinates for the constraint lines on the graph.
Material:
If X = 0, Y = 3,000
If Y = 0, X = 5,000
Labour:
If X = 0, Y = 4,000
If Y = 0, X = 4,000
In order to be able to plot the objective function (contribution) line you need to insert a figure to represent contribution into the formula and solve in the same way as the constraints.
Note: Select a figure for contribution which is easily divisible by your two contribution per unit figures – for example:
Let C = $60,000
If X = 0, Y = 1,500
If Y = 0, X = 2,000
Figure 1: Optimal production plan
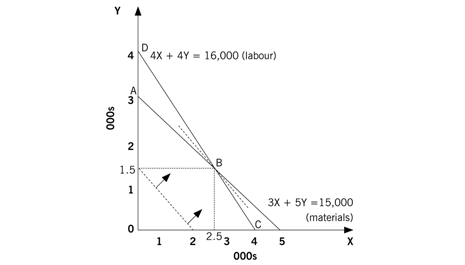
The area represented on the graph 0ABC is called the feasible region. Plotting the resulting graph will show that by pushing out the objective function to the furthest vertex in the feasible region which is along the gradient of the objective function, the optimal solution will be at point B – the intersection of materials and labour constraints. This is also the furthest vertex in the feasible region along the gradient of the objective function.
The optimal point is X = 2,500 and Y = 1,500, which generates $135,000 in contribution. Check this for yourself (Working 1). The ability to solve simultaneous equations is assumed in this article.
The point of this calculation is to provide management with a target production plan in order to maximise contribution and therefore profit. However, things can change and, in particular, constraints can relax or tighten. Management needs to know the financial implications of such changes. For example, if new materials are offered, how much should be paid for them? And how much should be bought? These dynamics are important.
Suppose the shadow price of materials is $5 per kg (this is verifiable by Working 2). The important point is, what does this mean? If management is offered more materials it should be prepared to pay no more than $5 per kg over the normal price. Paying less than $13 ($5 + $8) per kg to obtain more materials will make the firm better off financially. Paying more than $13 per kg would render it worse off in terms of contribution gained. Management needs to understand this.
There may, of course, be a good reason to buy ‘expensive’ extra materials (those costing more than $13 per kg). It might enable the business to satisfy the demands of an important customer who might, in turn, buy more products later. The firm might have to meet a contractual obligation, and so paying ‘too much’ for more materials might be justifiable if it will prevent a penalty on the contract. The cost of this is rarely included in shadow price calculations. Equally, it might be that ‘cheap’ material, priced at under $13 per kg, is not attractive. Quality is a factor, as is reliability of supply. Accountants should recognise that ‘price’ is not everything.
Students need to realise that as you buy more materials, then that constraint relaxes and so its line on the graph moves outwards and away from the origin. Eventually, the materials line will be totally outside the labour line on the graph and the point at which this happens is the point at which the business will cease to find buying more materials attractive (point D on the graph). Labour would then become the only constraint.
We need to find out how many materials are needed at point D on the graph, the point at which 4,000 units of Y are produced. To make 4,000 units of Y we need 20,000kg of materials. Consequently, the maximum amount of extra material required is 5,000kg (20,000 – 15,000).
Note: Although interpretation is important at this level, there will still be marks available for the basic calculations.
Working 1:
The optimal point is at point B, which is at the intersection of:
3X + 5Y = 15,000, and
4X + 4Y = 16,000
Multiplying the first equation by four and the second by three we get:
12X + 20Y = 60,000
12X + 12Y = 48,000
The difference in the two equations is:
8Y = 12,000, or Y = 1,500
Substituting Y = 1,500 in any of the above equations will give us the X value:
3X + 5 (1,500) = 15,000
3X = 7,500
X = 2,500
The contribution gained is (2,500 x 30) + (1,500 x 40) = $135,000
Working 2: Shadow price of materials
To find this we relax the material constraint by 1kg and resolve as follows:
3X + 5Y = 15,001 and
4X + 4Y = 16,000
Again, multiplying by four for the first equation and by three for the second produces:
12X + 20Y = 60,004
12X + 12Y = 48,000
8Y = 12,004
Y = 1,500.5
Substituting Y = 1,500.5 in any of the above equations will give us X:
3X + 5 (1,500.5) = 15,001
3X = 7,498.5
X = 2,499.5
The new level of contribution is: (2,499.5 x 30) + (1,500.5 x 40) = $135,005
The increase in contribution from the original optimal is the shadow price:
135,005 – 135,000 = $5 per kg.
Written by a member of the Performance Management examining team