Study guide references E3(g), (h) and (i) refer explicitly to the Internal Rate of Return (IRR). Not only do candidates need to be able to perform the calculation, they need to be able to explain the concept of IRR, how the IRR can be used for project appraisal, and to consider the merits and problems of this method of investment appraisal. In short, IRR can be examined in both a written or calculation format, within either section A or section B of the exam.
When this topic is examined, candidates have historically not performed very well, showing a lack of understanding of how the calculation works and what the IRR is.
The IRR can be defined as the discount rate which, when applied to the cash flows of a project, produces a net present value (NPV) of nil. This discount rate can then be thought of as the forecast return for the project. If the IRR is greater than a pre-set percentage target, the project is accepted. If the IRR is less than the target, the project is rejected.
Considering the definition leads us to the calculation. The IRR uses cash flows (not profits) and more specifically, relevant cash flows for a project. To perform the calculation, we need to take the cash flows of a project and calculate the discount factor that would produce a NPV of zero.
If the cash flows of a ‘normal’ (cash outflow followed by a series of cash inflows) project are taken and discounted at different discount rates, it will be possible to plot the following graph:
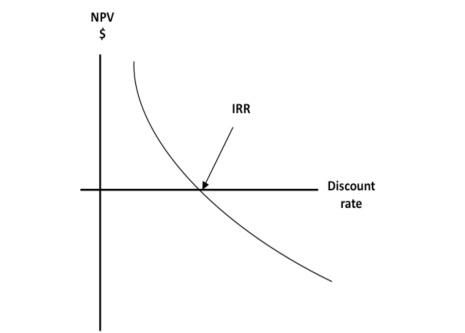
The discount rates used are on the x-axis, and the NPV ($) is on the y-axis. As you can see, the graph is a smooth curve, which crosses the x-axis. It is this point that we need to calculate the discount rate, which has produced a NPV of zero – this is the IRR.
It would be very time consuming to calculate the NPV of a project for many different discount factors and then plot the graph and estimate where the graph crosses the x-axis. Instead, there is a short cut using the formula:

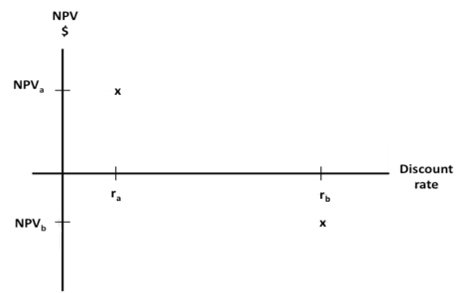
In order to use the formula then, we need to take the cash flows of the project and discount them twice – once using a discount rate a%, and once using a discount rate b%. If we plot these results on a graph it would be as follows:
We know that the line joining these two points should be a curve, but the formula approximates the curve with a straight line and so calculates the point at which a straight line crosses the x-axis and is therefore the IRR:
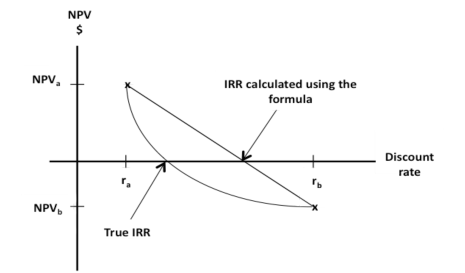
The estimation is most accurate if one NPV used in the formula is positive and the other one is negative. So if a candidate chooses a discount factor and calculates the NPV of the project which turns out to be negative, a lower discount rate should be chosen for the next discounting so that there is a possibility of obtaining a positive NPV. However, within an exam situation, if a candidate ends up with two positive or two negative NPVs, do not waste time calculating a third. Put the values you have into the formula and complete the calculation; no marks will be lost.
Let us put some figures in. A project has an immediate cash outflow of $7,000, and then cash inflows of $4,000 in years 1 and 2.
If we take the cash flows and discount them at 5% and 20%, the following results are gained. Note that in an exam situation a candidate could choose any discount rate to start with. In choosing the second discount rate, though, remember what was said above about trying to gain one positive and one negative NPV.
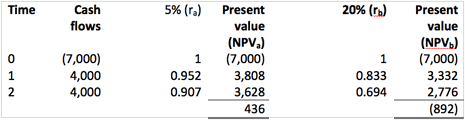
If these results are substituted into the formula:

Thus, the IRR is estimated to be 9.9%. This is the return that is forecast for the project. If the target return was 6%, then the project would be accepted; if the target return was 15%, then the project would be rejected.
As the cash inflows for the project are an annuity, there is actually a short cut that we can take for the calculation.
Let's set up the cash flows as an annuity:

For the discount factor (r%) to be the IRR, the NPV must be equal to zero. The table must look as follows:

Looking at the present value column, we can see that (7,000) + 4,000x AF1-2@r% = 0
Rearranging this gives 7,000/4,000 = AF1-2@r%
ie 1.75 = AF1-2@r%
Looking in the annuity tables, the rate with a two-year annuity closest to 1.75 is 9%.
While this answer is slightly different form the first answer gained, this is because we are always estimating the IRR, and different estimation methods will give slightly different answers. Either method would gain full marks in an exam context.
Candidates need to be able to explain the advantages and disadvantages of the IRR method of project appraisal.
Advantages
Disadvantages

If the decision was made purely on IRR, both projects would be ranked the same, and no decision could be made. However, looking at the size of the projects, Project 1 is larger and will generate greater cash flow and therefore profits for the organisation.
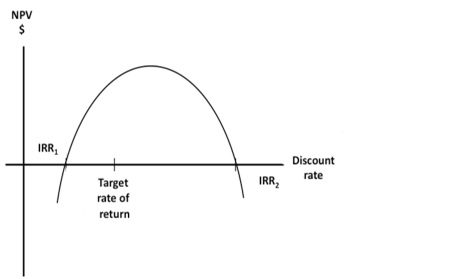
If only IRR 1 was calculated, then the project would be rejected as the target is higher, but if IRR 2 was calculated, the project would be accepted. So when a project has two IRRs, there is ambiguity as to whether the project should be accepted or not.
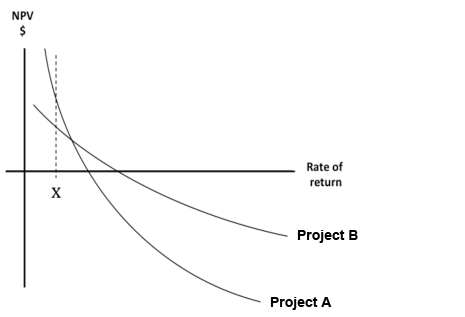
On an IRR basis, Project B should be chosen as the IRR is higher. But what if the organisation actually had a cost of capital of x%? We can see that Project A actually has the higher NPV at this point, and therefore Project A would increase the wealth of the shareholders by a greater amount, and should be chosen. So, with mutually exclusive projects, the IRR method can result in the wrong decision being made.
Candidates need to have a thorough grasp of the concept, the calculations and the advantages and disadvantages of the Internal Rate of Return. It is hoped that this article will help with these elements.
Written by a member of the Paper FFM examining team