This article addresses the learning outcomes from Performance Management (PM) syllabus area D: Material mix and yield variances and Analyse and evaluate past performance using the results of variance analysis.
Standard costing and basic variance calculations should be familiar from earlier studies. In PM, more advanced variances are introduced.
Recapping previous studies, the material usage variance is calculated as the difference between the actual material used for the production level achieved compared to the amount that was expected to be used, based on standard usage levels, valued at standard cost. This variance demonstrates if more or less material is used than expected.
When there is more than one input material, the material usage variance can be split into material mix and yield variances. When we talk about the materials ‘mix’ we are referring to the quantity of each material that is used to make our product – ie we are referring to our inputs. When we talk about ‘yield’, on the other hand, we are talking about how much of our product is produced – ie our output.
In many production processes, it may be possible to combine different levels (use a different mix) of the input materials to make the same product. This, in turn, may result in differing yields, depending on the mix of materials that has been used.
The material variances that can be calculated are therefore:

In a question, use either the usage variance or the mix and yield variances. To include both would be to double count. Also, do not forget the material price variance in your analysis as this may provide additional information. This is calculated as the difference between the actual quantity of material valued at the actual cost and the actual quantity of material valued at the standard cost.
EXAMPLE
We will use this past exam question to demonstrate the calculation of the variances and analysis of performance.
Requirement:
Calculate the material mix and yield variances and use these to discuss the performance of Kappa Co.
You have been given the standard mix of inputs. The standard proportions of the input materials is 40/120 of Alpha, 60/120 of Beta and 20/120 of Gamma for each 100kg of Omega.
You are also given the standard costs of each input material. The standard cost per kg of Alpha is $2, of Beta is $5 and of Gamma is $1. From this it can be seen that the more Beta used, the more expensive the final product will be.
It may be possible for the production manager to deviate from this standard mix and use slightly different proportions of each input material. The production manager may be tempted to replace some Beta for the cheaper Gamma as this would reduce the overall production cost.
When amending the mix, the production manager must take care however so as not to significantly affect the quality of the final product.
The material mix variance is calculated as the difference between the standard cost of the actual input materials in the actual mix used, compared to the standard cost of the actual input materials if the standard mix had been used.
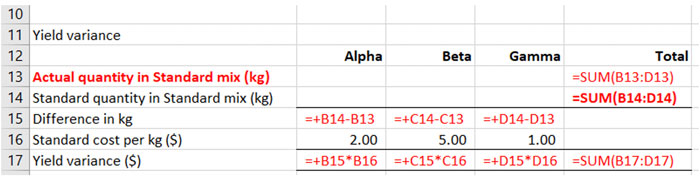
It is easier to calculate the material mix variance using a table format. In the exam you will be using the spreadsheet answer space for this type of answer which makes using the table layout even more compelling. You should be able to quickly set up your mix calculation table in the spreadsheet, including relevant formulae:
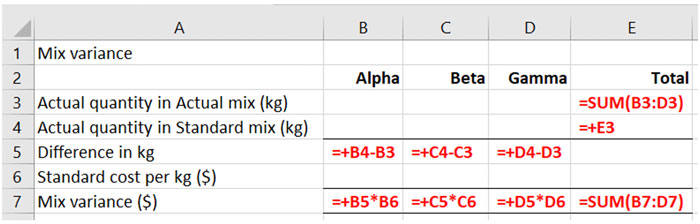
Once the table is set up you can start populating it.
The actual quantity in the actual mix is given in the question, as are the standard costs.
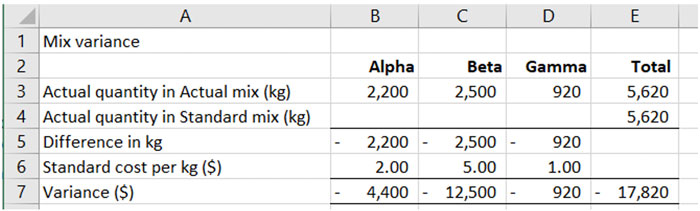
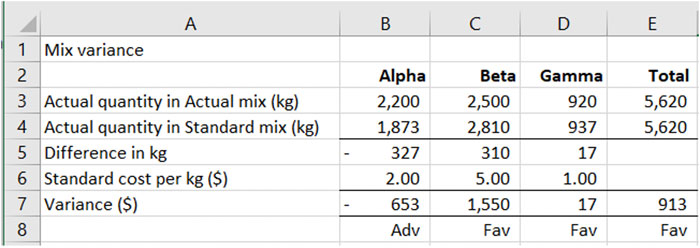
To complete the table, the actual quantity in the standard mix needs to be calculated using the standard proportions given in the question. In cells B4 to D4, calculate the amount of materials Alpha, Beta and Gamma that would have been used if the total quantity of 5,620kg had been input using the standard mix.

This completes the calculation of the mix variance, but remember, it is essential that, for every variance you calculate, to state whether it is favourable or adverse. This can be denoted as shown below (Adv or Fav), or by a clear ‘A’ or ‘F’. Avoid leaving your calculations as simply positive and negative figures as this leads to confusion and may not be awarded marks.
There are number of different ways to lay out a yield variance calculations. Any method can be used in the exam and will gain marks.
The material yield variance is calculated as the difference between the standard cost of the actual input materials in the standard mix, compared to the standard cost of the standard quantity of input materials in the standard mix.
The yield variance can be calculated using a similar table approach to the mix variance. To save time in the exam, copy down the mix variance table – but take care to make sure it is then set up correctly as there are some differences.
The main differences to note is in cell E14 which is now the sum of cells B14 to D14 and the heading for Actual quantity in standard mix is now on the top row of the table in cell A13. The standard costs can be left in the table.
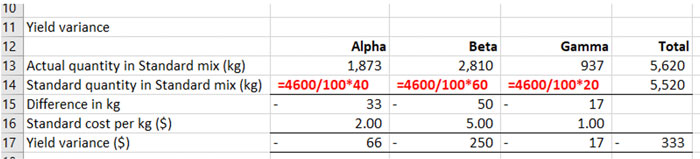
The values for actual quantity in standard mix can be copied down from the previous table.
To complete the table, calculate the standard quantity in the standard mix for each material. From the standard cost card, 40kg of Alpha is required for each 100kg of Alpha. Therefore, for the 4,600kg of Omega which was produced, it would have been expected that (4,600/100*40) = 1,840kg of Alpha would have been input. Similarly, (4,600/100*60) = 2,760kg of Beta and (4,600/100*20) = 920kg of Gamma would have been input.
This completes the calculation of the yield variance. Again, remember to clearly state if the variance is adverse or favourable.
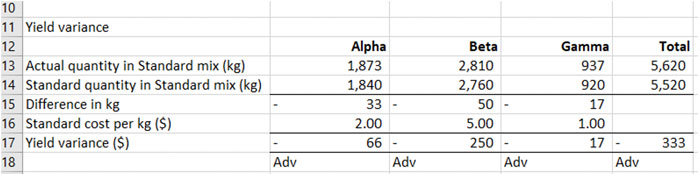
With the yield variance, we are really only interested in the total which is $333 Adverse. The yield variance can also be calculated at a total level:

There are other acceptable approaches. Find the approach that you prefer for the yield variance calculation and use this consistently.
If we add together the material mix and yield variances, we get a favourable usage variance of $580 ($913 – $333).
What do these calculations show about the performance of Kappa Co?
Over all there is a favourable mix variance. Looking at the individual variances, Gamma has a very small favourable variance. Beta has a large favourable variance and Alpha has a large adverse variance. Ignoring Gamma, we can focus our discussion on Alpha and Beta. Kappa Co has used relatively less of the more expensive material Beta, and relatively more of the cheaper material Alpha. Overall, the savings from using less Beta have outweighed the additional cost of the extra Alpha, thus resulting in a favourable total mix variance.
To answer this, we also have to consider the yield variance as the change in mix could have made the final product more difficult to produce or could have resulted in more wastage than if the standard mix had been used. There is a direct relationship between the materials mix variance and the materials yield variance and while using a mix of materials which was different from standard, it has resulted in a saving of $913·33, it has however led to an adverse yield variance of $580 due to the significantly lower yield that Kappa Co obtained than if it had used the standard mix of materials.
Of course, the adverse yield variance could have been caused by additional factors other than simply the change of mix, but in an exam answer unless those other factors are given, it is acceptable to assume that the change in the mix has been the main reason for the lower yield.
The overall usage variance reported shows a $580 favourable variance, so it could be viewed that the change in the mix had a favourable impact overall.
For Kappa Co, if the only variance calculated was the favourable usage variance, then it would be assumed that the production manager had demonstrated a good performance and obtained more efficient production. When the mix and yield variances are considered, it is clear that the positive usage variance is caused by a change in the mix of inputs. It will need to be considered what impact this change of mix has had on the quality of the finished product and ultimately on sales. Again, this should be considered where information concerning this has been provided in the question.
In an analysis question involving variances, it is important to consider who is responsible for the variances. Some information on this should be provided in the question. For Kappa Co it is worth noting that the standards set are not the responsibility of the production manager. Also, as they are out of date (they were calculated five years ago), this could be contributing to the variances calculated.
In general, it can be assumed in exam questions that the production manager is responsible for the mix of input materials used. It can be tempting for production managers to change the product mix in order to make savings; these savings may lead to greater bonuses for them at the end of the day. However, if the quality of the product is adversely affected, this is damaging to the reputation of the business and hence its long‑term survival prospects. While substituting lower quality or cheaper input materials may in some cases lead to yield volumes that are the same as those achieved with higher quality materials, the yield may not be of the same quality.
For a full appreciation of the impact of the mix change, the sales variances would also have to be considered, although it is likely to take time for sales volumes to be affected. Any sales volume variance that does arise as a result of poor quality products is likely to arise in a different period from the one in which the mix and yield variances arose, and the correlation will then be more difficult to prove.
Similarly, poorer quality materials may be more difficult to work with; this may lead to an adverse labour efficiency variance as the workforce takes longer than expected to complete the work. This, in turn, could lead to higher overhead costs, and so on.
Fortunately, consequences such as these will occur in the same period as the mix variance and are therefore more likely to be identified and the problem resolved.
Never underestimate the extent to which a perceived ‘improvement’ in one area (for example, a favourable materials mix variance) can lead to a real deterioration in another area (for example, decreased yield, poorer quality, higher labour costs, lower sales volumes, and ultimately lower profitability). Always make sure you mention such interdependencies when discussing variances in exam questions.
Written by a member of the Performance Management examining team