Inventory control features in the syllabuses of several ACCA exams. The areas usually tested in these exams are:
- determining an economic order quantity (EOQ) – calculations to assess how many units of a particular inventory item to order at a time
- finding an optimal re-order level (optimal ROL) – providing some idea of the level to which inventories can be allowed to fall before placing an order for more
- discussions of various practical aspects of inventory management – often referred to by students with no practical experience as ‘theory’.
Advantages and disadvantages of holding inventory
The basis of the theoretical calculations of an EOQ and an optimal ROL is that there are advantages and disadvantages of holding inventory (of buying inventory in large or small quantities). The advantages include:
- the need to meet customer demand
- taking advantage of bulk discounts
- reducing total annual re-ordering cost
The disadvantages include:
- storage costs
- cost of capital tied up in inventory
- deterioration, obsolescence, and theft
The aim behind the calculations of EOQ and ROL is to weigh up these; and other advantages and disadvantages and to find a suitable compromise level.
EOQ
When determining how much to order at a time, an organisation will recognise that:
- as order quantity rises, average inventory rises and the total annual cost of holding inventory rises
- as order quantity rises, the number of orders decreases and the total annual re-order costs decrease.
The total of annual holding and re-order costs first decreases, then increases. The point at which cost is minimised is the EOQ. This cost behaviour is illustrated by the graph in Figure 1.
Figure 1
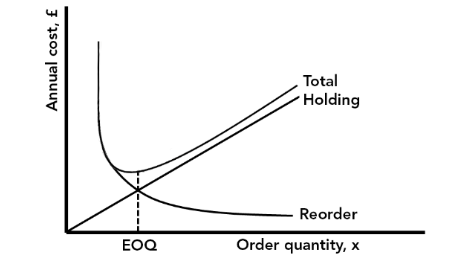
The way in which this EOQ is calculated is based on certain assumptions, including:
- constant purchase price
- constant demand and constant lead-time
- holding-cost dependent on average inventory
- order costs independent of order quantity
The assumptions result in a pattern of inventory that can be illustrated graphically as shown in Figure 2.
Figure 2
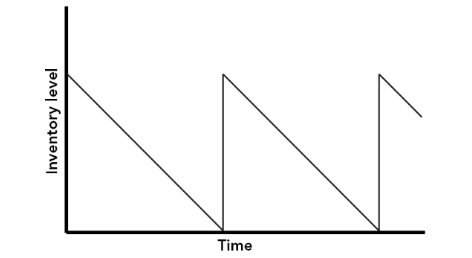
The formula
Using the standard ACCA notation in which:
CH = cost of holding a unit of inventory for a year
CO = cost of placing an order
D = annual demand
also:
TOC = total annual re-ordering cost
THC = total annual holding cost
Q = order quantity
then:
average inventory = Q/2
THC = Q/2 × CH
and:
number of orders in a year = D/Q
TOC = D/Q × CO
The total annual cost (affected by order quantity) is:
C = THC + TOC = Q/2 × CH + D/Q × CO
This formula is not supplied in exams – it needs to be understood (and remembered).
The value of Q, order quantity, that minimises this total cost is the EOQ, given by an easily remembered formula:
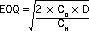
Use of EOQ Formula
You need to take care over which figures you put into the formula, particularly in multiple-choice questions. The areas to beware of fall into two categories:
- Relevant costs – only include those costs affected by order quantity. Only include those holding costs which (in total in a year) will double if you order twice as much at a time. (Thus, fixed salaries to storekeepers or buying department staff will be excluded.)
- Consistent units – ensure that figures inserted have consistent units. Annual demand and cost of holding a unit for a year. Both holding costs and re-ordering costs should be in $, or both in cents.
Bulk Discounts
A common twist to exam questions is to ask students to evaluate whether bulk discounts are worth taking. While prices reduce, total annual holding costs will increase if more inventory is ordered at a time, so the matter needs a little thought.
The common approach is one of trial and error. This involves finding the total annual cost (holding cost, re-ordering cost and purchasing cost) at the level indicated by the EOQ and at the level(s) where discount first becomes available.
Figure 3 shows total costs (now including cost of purchasing the inventory) plotted against order quantity with discount incorporated.
Figure 3
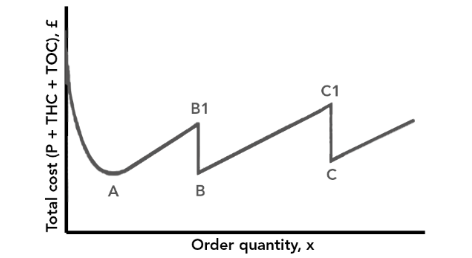
Point A represents the cost at the order quantity indicated by the EOQ. If inventory is ordered in larger quantities, total costs will increase to point B1, at which stage bulk discounts are available, bringing the costs down to point B. Any calculations will involve finding which cost out of A, B or C is the lowest, as Example 1 will show.
Example 1
Moore Limited uses 5,000 units of its main raw material per month. The material costs $4 per unit to buy, supplier’s delivery costs are $25 per order and internal ordering costs are $2 per order. Total annual holding costs are $1 per unit. The supplier has offered a discount of 1% if 4,000 units of the material are bought at a time.
Required:
- Establish the economic order quantity (EOQ) ignoring the discount opportunities.
- Determine if the discount offer should be accepted.
Example 1 solutions
1. EOQ = √(2 x Co x D)/Ch
Where:
D - annual demand = 5,000 x 12 = 60,000 units
Co – order cost = $25 + $2 = $27 per order
Ch – holding cost = $1 per unit
EOQ = √(2 x 27 x 60,000)/1 = 1,800 units
2. Should the discount be accepted?

On financial grounds, the discount should be accepted as the total cost would be $1,795 less. However, consideration would have to be given to whether the company can accommodate the larger order size in terms of storage.
Re-order levels
As important as how much to order at a time is the question of when to order more inventory. If an order is placed too late, when inventories have been allowed to run too low, a ‘stock-out’ will occur, resulting in either a loss of production or loss of sales, or possibly both.
If orders are placed too soon, when there are still substantial supplies in inventory, then inventory levels and holding costs will be unnecessarily high. The re-order level as explained below should not be confused with the inventory control levels referred to in textbooks – this article ignores these. When it comes to calculating re-order levels, three sets of circumstances can be envisaged.
Lead-time is zero
‘Lead-time’ is the interval between placing an order with a supplier and that order arriving. It is unlikely that this could be reduced to zero – it would require astonishingly co-operative and efficient suppliers. If it were possible, a re-order level of zero could be adopted. An organisation could simply wait until it ran out of inventory, click its corporate fingers, and inventory would arrive instantaneously.
Constant demand, fixed finite lead-time
The assumption of constant demand is consistent with the assumptions underlying the EOQ formula. If suppliers take some time to provide goods, orders need to be placed in advance of running out. Figure 4 illustrates the problem and its solution.
Figure 4
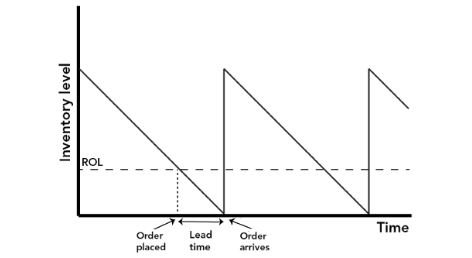
If the lead-time is, say, five days, an order has to be placed before inventories have been exhausted. Specifically, the order should be placed when there is still sufficient inventory to last five days, ie:
Re-order level (ROL) = Demand in lead-time
So, if lead-time for a particular inventory item is five days and daily demand is 30 units, the re-order level would be five days at 30 units per day, 150 units.
Buffer inventory
Buffer inventory is simply the amount by which ROL exceeds average demand in lead-time. It is needed when there is uncertainty in lead-time demand to reduce the chance of running out of inventory and reduce the cost of such shortages.
Optimal re-order levels
This leaves the problem of how to calculate the optimal ROL. There are two common ways in which one could determine a suitable re-order level (if the information was available):
- A tabular approach – Calculate, for each possible ROL (each level of buffer inventory) the cost of holding different levels of buffer inventory and the cost incurred if the buffer is inadequate (‘stock-out’ costs). The optimal re-order level is that level at which the total of holding and stock-out costs are a minimum.
- A ‘service level’ approach – An organisation has to determine a suitable level of service (an acceptably small probability that it would run out of inventory), and would need to know the nature of the probability distribution for lead-time demand. These two would be used to find a suitable ROL.
Written by a member of the Management Accounting examining team


