Examining team guidance on time apportioning
Several areas of the Financial Management syllabus, such as ‘explain and apply the characteristics and role of the principal money market instruments’ (section B3) and ‘hedging techniques for foreign currency’ and ‘interest rate risk’ (area G) require either annualising or short-term pro-rating of percentage figures. There are two alternative approaches for this and the approach chosen can affect calculations in questions in both of these areas of the Financial Management syllabus. The purpose of this article is to explain these approaches and clarify ACCA’s preferred approach.
EXAMPLE 1
The following question was published in the June 2019 examiner report
A listed company is to enter into a sale and repurchase agreement on the money market.
The company has agreed to sell $10m of treasury bills for $9.6m and will buy them back in 50 days' time for $9.65m.
Assume a 365-day year.
What is the implicit annual interest rate in this transaction (to the nearest 0.01%)?
The alternative approaches can be summarised as follows:
METHOD 1
The percentage figure is multiplied by a fraction representing either the period to be pro-rated or the period which requires annualisation. This can be on either a daily or a monthly basis, depending on how the information is presented in the question.
The calculation using method 1 is as follows:
Increase in value = $9.65m – $9.6m = $0.05m
As a percentage of the original value = $0.05m/$9.6m = 0.52%
Annualising this value = 0.52% x 365/50 = 3.80%.
The annualisation here, has been done by multiplying by the number of days in the year and dividing by the number of days in the period in the question. To annualise a figure for a monthly period, it would be necessary to multiply by the number of months in the year and divide by number of months in the period in the question eg x 12/5 for a five-month period.
Using a similar method, pro-rating an annual figure, such as using an annual interest rate to get a three-month interest rate, would involve multiplying by 3/12 (see example 2 below).
METHOD 2
The percentage figure is raised to the power of a fraction representing either the period to be pro-rated or the period which requires annualisation. This can also be on either a daily or a monthly basis.
Using the same example, the calculation using method 2 is as follows:
Increase in value = $9.65m – $9.6m = $0.05m
As a percentage of the original value = $0.05m/$9.6m = 0.52%
Annualising this value = (1 + 0.0052) ^ (365/50) – 1 = 3.86%.
EXAMPLE 2
For a further example considering money market hedging, the case Marigold, which was published in the Sept/Dec 2020 examiner report contains the following:
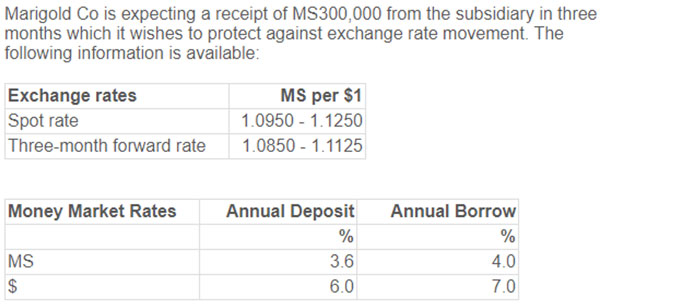

METHOD 1
Using method 1 the answer is as follows:
Borrowing rate pro-rated for three months = 4% x 3/12 = 1%
Amount to borrow = MS300,000 / 1.01 = MS297,030
Amount to deposit = MS297,030 / MS1.1250 = $264,027
METHOD 2
Borrowing rate for three months = (1 + 0.04) ^ 3/12 – 1 = 0.99%
Amount to borrow = MS300,000 / 1.0099 = MS297,059
Amount to deposit = MS297,059 / MS1.1250 = $264,052
Advice to candidates
Apart from risk management calculations, the advice from the examining team is to use method 2 in all areas of the FM syllabus since, strictly speaking, this is the technically correct method for annualising interest rates even though, in certain instances, method 1 can provide a useful approximation.
However, all questions involving risk management calculations in the Financial Management exam will be assessed using method 1 because this is simpler and will take less time than method 2.
Written by a member of the Financial Management examining team


