Bond valuation and bond yields

Bonds and their variants such as loan notes, debentures and loan stock, are IOUs issued by governments and corporations as a means of raising finance. They are often referred to as fixed income or fixed interest securities, to distinguish them from equities, in that they often (but not always) make known returns for the investors (the bond holders) at regular intervals. These interest payments, paid as bond coupons, are fixed, unlike dividends paid on equities, which can be variable. Most corporate bonds are redeemable after a specified period of time. Thus, a ‘plain vanilla’ bond will make regular interest payments to the investors and pay the capital to buy back the bond on the redemption date when it reaches maturity.

This article, the first of two related articles, will consider how bonds are valued and the relationship between the bond value or price, the yield to maturity and the spot yield curve. It addresses, in part, the learning required in Sections B3a and B3e of the the Advanced Financial Management Syllabus and Study Guide.

Bond value or price

Example 1
How much would an investor pay to purchase a bond today, which is redeemable in four years for its nominal value or face value of $100 and pays an annual coupon of 5% on the nominal value? The required rate of return (or yield) for a bond in this risk class is 4%.

As with any asset valuation, the investor would be willing to pay, at the most, the present value of the future income stream discounted at the required rate of return (or yield). Thus, the value of the bond can be determined as follows:

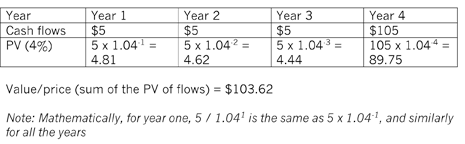
If the required rate of return (or yield) was 6%, then using the same calculation method, the price of the bond would be $96.53. And where the required rate of return (or yield) is equal to the coupon – 5% in this case – the current price of the bond will be equal to the nominal value of $100.

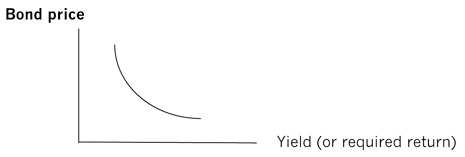
Thus, there is an inverse relationship between the yield of a bond and its price or value. The higher rate of return (or yield) required, the lower the price of the bond, and vice versa. However, it should be noted that this relationship is not linear, but convex to the origin.

The plain vanilla bond with annual coupon payments in the above example is the simpler type of bond. In addition to the plain vanilla bond, candidates – as part of their Advanced Financial Management studies and exam – are required to have knowledge of, and be able to deal with, more complicated bonds such as: bonds with coupon payments occurring more frequently than once a year; convertible bonds and bonds with warrants which contain option features; and more complicated payment features such as repayment mortgage or annuity type payment structures.

Yield to maturity (YTM) (also known as the [Gross] Redemption Yield (GRY))
If the current price of a bond is given, together with details of coupons and redemption date, then this information can be used to compute the required rate of return or yield to maturity of the bond.

Example 2
A bond paying a coupon of 7% is redeemable in five years at nominal value ($100) and is currently trading at $106.62. Estimate its yield (required rate of return).

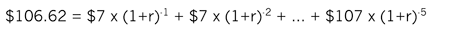
The internal rate of return approach can be used to obtain r. Since the current price is higher than $100, r must be lower than 7%.

Initially, try 5% as r:

$7 x 4.3295 [5%, five - year annuity] + $100 x 0.7835 [PV 5%, five - year] = $30.31 + $78.35 = $108.66

Try 6% as r:
$7 x 4.2124 [6%, five - year annuity] + $100 x 0.7473 [PV 6%, five - year] =
$29.49 + $74.73 = $104.22

Yield = 5% + (108.66 – 106.62 / 108.66 – 104.22) x 1% = 5.46%

The 5.46% is the yield to maturity (YTM) (or redemption yield) of the bond. The YTM is the rate of return at which the sum of the present values of all future income streams of the bond (interest coupons and redemption amount) is equal to the current bond price. It is the average annual rate of return the bond investors expect to receive from the bond till its redemption. YTMs for bonds are normally quoted in the financial press, based on the closing price of the bond. For example, a yield often quoted in the financial press is the bid yield. The bid yield is the YTM for the current bid price (the price at which bonds can be purchased) of a bond.

Term structure of interest rates and the yield curve
The yield to maturity is calculated implicitly based on the current market price, the term to maturity of the bond and amount (and frequency) of coupon payments. However, if a corporate bond is being issued for the first time, its price and/or coupon payments need to be determined based on the required yield. The required yield is based on the term structure of interest rates and this needs to be discussed before considering how the price of a bond may be determined.

It is incorrect to assume that bonds of the same risk class, which are redeemed on different dates, would have the same required rate of return or yield. In fact, it is evident that the markets demand different annual returns or yields on bonds with differing lengths of time before their redemption (or maturity), even where the bonds are of the same risk class. This is known as the term structure of interest rates and is represented by the spot yield curve or simply the yield curve.

For example, a company may find that if it wants to issue a one - year bond, it may need to pay interest at 3% for the year, if it wants to issue a two - year bond, the markets may demand an annual interest rate of 3. 5%, and for a three-year bond the annual yield required may be 4.2%. Hence, the company would need to pay interest at 3% for one year; 3.5% each year, for two years, if it wants to borrow funds for two years; and 4.2% each year, for three years, if it wants to borrow funds for three years. In this case, the term structure of interest rates is represented by an upward sloping yield curve.

The normal expectation would be of an upward sloping yield curve on the basis that bonds with a longer period of maturity would require a higher interest rate as compensation for risk. Note here that the bonds considered may be of the same risk class but the longer time period to maturity still adds to higher uncertainty.

However, it is entirely normal for yield curves to be of many different shapes dependent on the perceptions of the markets on how interest rates may change in the future. Three main theories have been advanced to explain the term structure of interest rates or the yield curve: expectations hypothesis, liquidity-preference hypothesis and market-segmentation hypothesis. Although it is beyond the remit of this article to explain these theories, many textbooks on investments and financial management cover these in detail.

Valuing bonds based on the yield curve
Annual spot yield curves are often published by the financial press or by central banks (for example, the Bank of England regularly publishes UK government bond yield curves on its website). The spot yield curve can be used to estimate the price or value of a bond.

Example 3
A company wants to issue a bond that is redeemable in four years for its nominal value or face value of $100, and wants to pay an annual coupon of 5% on the nominal value. Estimate the price at which the bond should be issued.

The annual spot yield curve for a bond of this risk class is as follows:
One-year             3.5%
Two-year             4.0%
Three-year          4.7%
Four-year            5.5%

The four-year bond pays the following stream of income:

Year                     1             2             3             4
Payments            $5           $5           $5           $105

This can be simplified into four separate bonds with the following payment structure:

Year                     1             2             3             4
Bond 1                 $5
Bond 2                               $5
Bond 3                                               $5
Bond 4                                                             $105

Each annual payment is a single payment in that particular year, much like a zero-coupon bond, and its present value can be determined by discounting each cash flow by the relevant yield curve rate, as follows:

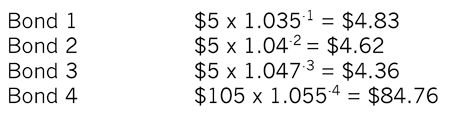
The sum of these flows is the price at which the bond can be issued, $98.57.

The yield to maturity of the bond is estimated at 5.41% using the same methodology as example 2.

Some important points can be noted from the above calculation; firstly, the 5.41% is lower than 5.5% because some of the ret urns from the bond come in earlier years, when the interest rates on the yield curve are lower, but the largest proportion comes in Year 4. Secondly, the yield to maturity is a weighted average of the term structure of interest rates. Thirdly, the yield to maturity is calculated after the price of the bond has been calculated or observed in the markets, but theoretically it is term structure of interest rates that determines the price or value of the bond.

Mathematically:

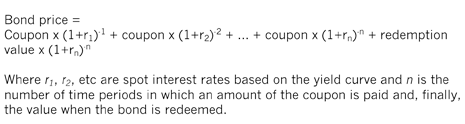
In this article it is assumed that coupons are paid annually, but it is common practice to pay coupons more frequently than once a year. In these circumstances, the coupon payments need to be reduced and the time period frequency needs to be increased.

Estimating the yield curve
There are different methods used to estimate a spot yield curve, and the iterative process based on bootstrapping coupon paying bonds is perhaps the simplest to understand. The following example demonstrates how the process works.

Example 4
A government has three bonds in issue that all have a face or nominal value of $100 and are redeemable in one year, two years and three years respectively. Since the bonds are all government bonds, let’s assume that they are of the same risk class. Let’s also assume that coupons are payable on an annual basis. Bond A, which is redeemable in a year’s time, has a coupon rate of 7% and is trading at $103. Bond B, which is redeemable in two years, has a coupon rate of 6% and is trading a t $102. Bond C, which is redeemable in three years, has a coupon rate of 5% and is trading at $98.

To determine the yield curve, each bond’s cash flows are discounted in turn to determine the annual spot rates for the three years, as follows:

The annual spot yield curve is therefore:

Year
      1    3.88%
      2    4.96%
      3    5.80%

Discussion of other methods of estimating the spot yield curve, such as using multiple regression techniques and observation of spot rates of zero coupon bonds, is beyond the scope of the Advanced Financial Management syllabus.

As stated in the previous section, often the financial press and central banks will publish estimated spot yield curves based on government issued bonds. Yield curves for individual corporate bonds can be estimated from these by adding the relevant spread to the bonds. For example, the following table of spreads (in basis points) is given for the retail sector.

Rating         1 year         2 year         3 year
AAA            14               25               38
AA               29              41               55
A                 46              60               76

Example 5
Mason Retail Co has a credit rating of AA, then its individual yield curve – based on the government bond yield curve and the spread table above – may be estimated as:

Year 1            Year 2             Year 3
4.17%            5.37%             6.35%

These would be the rates of return an investor buying bonds issued by Mason Retail Co would expect, and therefore Mason Retail Co would use these rates as discount rates to estimate the price or value of coupons when it issues new bonds. And Mason Retail Co’s existing bonds’ market price would reflect its individual yield curve.

Conclusion
This article considered the relationship between bond prices, the yield curve and the yield to maturity. It demonstrated how bonds can be valued and how a yield curve may be derived using bonds of the same risk class but of different maturities. Finally it showed how individual company yield curves may be estimated.

A following article will discuss how forward interest rates are determined from the spot yield curve and how they may be useful in determining the value of an interest rate swap. It will address the learning required in Sections E1 and E3 of the Advanced Financial Management Syllabus and Study Guide.

Written by the Advanced Financial Management examining team