While the use of real options in investment appraisal is increasingly accepted, the practicalities of using option pricing techniques and ideas in making actual financial strategy decisions is less well understood.
This article will initially consider how an individual traditional project could be reassessed using option valuation. It will then consider how option valuation could assist when assessing a portfolio of projects and will conclude with a brief discussion regarding inter-dependent projects.
A traditional project and option valuation
Let us imagine that a company is proposing a major expansion project. The operational management team have forecast the cash flows relevant to the project in line with the standard assumptions and policies set down by the financial management. The financial management have then discounted these cash flows at a cost of capital of 11% and this has resulted in an NPV of just $5m. For the sake of simplicity tax, inflation and other real world complications have been ignored.
NPV calculation – overall:
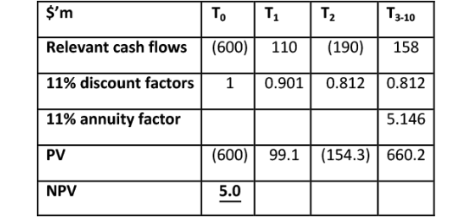
Those executives who are keen proponents of this expansion are disappointed by the low NPV and fear that the project is unlikely to win approval when competing for funds against other projects. They consider that the project is being undervalued and, hence, a meeting with the financial management team is arranged. At this meeting the financial management team query the large net cash outflow that is forecast to occur at the end of year two. As a result of this, it becomes apparent that the project comprises an initial investment of $600m which will produce net cash inflows of $110m for the following 10 years, followed by a further investment of $300m after two years which will increase the net cash inflows by $48m to $158m per year for the remaining eight years. Further discussion reveals that the additional investment after two years is discretionary and does not necessarily need to be made.
Hence, the project could be viewed as an initial expansion costing $600m – phase 1 – followed by an option to expand further after two years – phase 2.
If separate NPV calculations are carried out for each of these phases. The results below are obtained.
NPV calculation – phase 1:
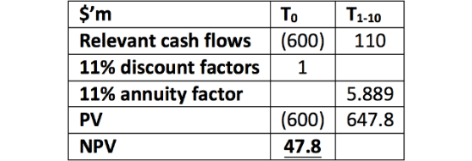
NPV calculation – phase 2:
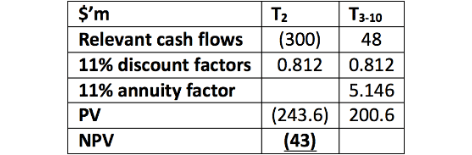
The total NPV is fundamentally unchanged as $47.8m – $43m = $4.8m, which is about the same as the $5m calculated initially. To the extent there is a difference, this can be attributed to rounding. This analysis alone provides some insight as, given that there is no obligation for the company to carry out phase two, the overall NPV must be at least $47.8m which far exceeds the initial NPV calculated of $5m.
It is worth noting that the discretionary spend at the end of year two has also been discounted at the 11% cost of capital. Although this is the approach commonly taken it could be more accurate to discount such discretionary expenditure at the risk free rate. This is because discretionary expenditure has much less operational risk than the net cash inflows that it is hoped will arise from such expenditure. If a risk free rate of 5% is used the present value of the $300m expenditure at the end of year two would be $272.1m. This is $28.5m (272.1 – 243.6) more than the present value if the cost of capital is used. Hence, the original overall NPV and the NPV of phase two should perhaps be reduced by this $28.5m. This approach would be consistent with the treatment of the exercise price in the Black Scholes Option Pricing model.
Although phase two does not currently seem worthwhile the option to carry out this phase can only add value as an option can never have a negative value. If the cash flows expected from phase two were to become favourable, the company will have the ability to carry out phase two and reap the benefit. Hence, the overall NPV will be $47.8m plus the value of the option to carry out phase two.
In order to value the option to carry out phase two we must first attribute figures to the inputs required for the Black Scholes option pricing (BSOP) formula:
- Pe = the investment required after two years to carry out phase two = $300m
- Pa = the PV of the net cash inflows currently forecast to arise from phase two = $200.6m (this must exclude the Pe)
- t = the time until phase two will begin = 2 years
- s = the volatility – assumed to be 0.4 (standard deviation)
- r = the risk free rate – assumed to be 5%
The Pe and Pa figures can be seen in the calculation of the NPV for phase two and, as we know, the company has the option to expand into phase two after two years. The s and r will both be given within any exam question and, hence, suitable figures have been assumed.
Using these inputs into the BSOP calculator given in the exam will give the following:
Option value:
d1 = 0.2519
d2 = – 0.8175
N(d1) = 0.4006
N(d2) = 0.2068
c = $24.22m
p = $95.07m
An option to expand (or follow-on) is a type of call option. Hence, the total NPV for the project with the option to expand = $47.8m + $24.22m = $72.02m. As a result of the financial management taking the time to better understand the project and the real options within it a project which seemed fairly marginal, has been shown to be attractive and is far more likely to win approval.
The attractiveness of the project arises because phase one of the project is itself attractive and the company can potentially benefit if the phase two expansion finally becomes worthwhile.
As discussed in the previous real options article, there are significant problems associated with using BSOP to value real options and, hence, the option value of $24.22m calculated should be treated as indicative only and should be used with care.
A portfolio of projects and option valuation
As soon as executives launch a strategy conditions change in the environment within which they are operating and indeed their knowledge of that environment is updated. Hence, managers must actively manage and respond accordingly. Traditional NPV analysis is probably too static a tool to reflect this active management. This is because it tends to assume a company will follow a previously agreed plan and does not account so well for how events may unfold. Instead managers should perhaps view the projects they could undertake to achieve their goals as a portfolio of real options which they could potentially exercise over time.
Imagine a company is faced with six independent projects as follows:
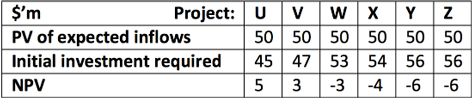
Given this basic NPV analysis projects U and V would be accepted and a total NPV of $8m would be generated for the company.
Let us now imagine that projects U and X have to be carried out immediately or not at all. In other words there is no option to delay these projects. Hence, project U would be accepted to generate an NPV of $5m and project X would be rejected. A useful analogy here is that of fruit growing in a garden. Projects U and X represent fruits which have to be picked now. Project U represents the perfectly ripe fruit which can be sold or eaten, while project X represents the rotten fruit which must be picked but then discarded.
The remaining projects can be delayed and represent fruits which do not have to be picked immediately and which have the potential to develop into perfectly ripe fruit. Given the volatility of the cash flows from these projects and the period by which they could be delayed option values can be calculated for these projects. This data and the resulting option values are presented below:
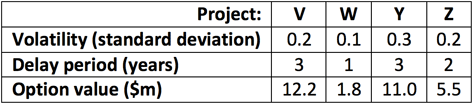
These option values have been calculated using an assumed risk free rate of 5%.
These option values total to a value of $30.5m. If the NPV of project U, which has already been accepted, is added to this a total value of $35.5m is created. This value is significantly higher than the original NPV of $8m which could have been generated by accepting projects U and V. However, careful management is necessary if as much value as possible is to be generated.
We will now consider each of projects V, W, Y and Z separately:
Project V:
This project looks most promising. It has a positive NPV if exercised now but its value as an option is significantly higher. Hence, exercising now would appear sub-optimal as with further nurturing a higher value could be generated. To continue the fruit analogy this project represents a fruit which could be picked now and eaten or sold but which, with careful cultivation, could become a larger and better fruit. However, just as ripening fruit can be eaten by pests, there is potential for project value to be lost – through the actions of competitors for instance. Hence, the company may decide to exercise the option early to realise the existing positive NPV.
Project W:
This project is not at all promising. It has a negative NPV if exercised now and, as it has a low volatility and there is a relatively short time until a decision has to be made regarding this project, it has a low option value. Hence, this project will probably never be worth exercising. This project could be thought of as the small, late developing fruit which is unlikely to ripen before the season ends.
Project Y:
Despite currently having a negative NPV this project has a high value as an option. This is due to the fact that it will not expire for three years and has a relatively high volatility when compared to the other projects. Hence, this project will probably be worth exercising at some later date. This project represents the unripe fruit which cannot be picked now, but which is expected to mature into a perfectly ripe fruit in the future.
Project Z:
This project is similar to project Y but is much less promising. It currently has the same negative NPV as project Y but as it has a lower volatility and a shorter time until it expires it has a lower value as an option when compared to project Y. This project seems unlikely to be worth exercising but there is still a reasonable chance that it could move ‘into the money’ and, hence, may become worth exercising in the future. As with project Y this project is also an unripe fruit which cannot be picked now. However, its chances of maturing into a perfectly ripe fruit seem much less.
How does the use of option valuation analysis help when compared to a traditional NPV analysis?
As previously stated traditional NPV analysis would lead to the acceptance of projects U and V, resulting in an NPV of $8m, and the rejection of the other four projects. However, option valuation analysis results in the acceptance of project U generating an NPV of $5m, the rejection of project X and options to carry out the four other projects in the future the total value of which has been estimated as $30.5m.
Further the analysis encourages active management:
Project V has been identified as worthy of careful management to ensure it is carried out at the optimal time to maximise the value created but at the same time ensuring that the existing positive NPV is not destroyed.
Of the remaining projects Project W has been identified as the project deserving least attention while with careful nurturing project Y and even project Z could finally create value for the company.
It is crucial to recognise that projects, just like fruit, do require nurturing. This is because as the time approaches when the project must be carried out or abandoned, the option value will always tend to decline assuming all other variables remain constant. This is because the time to maturity falls and the present value of the exercise price, the investment to be made to carry out the project, is rising.
Hence, without nurturing all the option values will move to zero over time. For this not to happen there must be good luck or active management. Good luck could add value to a project because, for instance, sudden growth in the economy could mean the returns from a project become higher than originally forecast. Active management could involve taking action to reduce the costs or increase the revenues associated with a project. Equally action could be taken to reduce the initial investment required in the project.
Using the option valuation approach has helped identify those projects most likely to benefit from such nurturing and, hence, is useful as a company follows and develops its financial strategy.
Inter-dependent projects
So far this article has looked at how our understanding of a single project and a portfolio of independent projects could be enhanced by the use of option valuation. Let us now consider briefly interdependent projects.
Just as you and I are faced with a myriad of options when buying a new car the car manufacturer also has many options.
For instance a car manufacturer may have a project to launch a new saloon model. From this saloon model, an estate model could then be launched, and from this a 4x4 version of the estate model could be launched. This is a strategy followed by Skoda with their Octavia and Superb ranges. In effect the company has the initial project (the launch of the saloon), followed by a call option on the launch of the estate, which itself has a call option on the launch of the 4x4 estate. Hence, the company has a call on a call! This is known as a nest of options or nested options.
Another car manufacturer may also have a project to launch a new saloon model. From this saloon, an estate model could be launched and a sports utility vehicle (SUV) model could also be launched. This is a strategy followed by BMW with their 3 series and 5 series ranges. In effect the company has the initial project (the launch of the saloon), followed by a call option on the launch of the estate and a call option on the launch of the SUV model (the BMW X3 and X5). While these options are not nested they are obviously still very much related.
Understanding how these options inter-relate is obviously useful to a company as they develop their strategy. Once again good luck and active management play their part. For instance a few bad winters is likely to enhance future sales of SUV’s and 4x4 estates. This in turn enhances the value of the call options to manufacture these models and, hence, the value of the original product launch.
Active management could involve the development of a new more fuel efficient 4x4 system. Any such increase in fuel efficiency is also likely to enhance the sales of 4x4 equipped SUV’s and estates, and enhance the value of the call options to manufacture these models and, hence, the value of the original product launch. Conversely, extra sales of 4x4 equipped models may reduce sales of other models.
Obviously the initial product launch should be marketed in such a way as to maximise its success. Active management should also ensure that this initial product launch should ensure consumers’ perception of the new model is developed in such a way that the chances of success of the follow on models is optimised.
Our knowledge of the determinants of option values can also be useful. For instance if sales of SUV’s are high in a more volatile market such as China this adds value to the option to develop the SUV variant of the model in the future, and, hence, enhances the value of the initial project to launch the saloon.
Conclusion
This article has demonstrated how option valuation techniques can help understand the potential value of projects and how financial strategy decisions can be made using this knowledge in order to maximise the results arising from projects and, hence, maximise company value.
William Parrott, freelance tutor and senior FM tutor, MAT Uganda
References
- Investment Opportunities as Real Options: Getting Started on the Numbers
- Timothy A. Luehrman, Harvard Business Review, July/August 1998
- Strategy as a Portfolio of Real Options
- Timothy A. Luehrman, Harvard Business Review, September/October 1998


