Cost-volume-profit analysis looks primarily at the effects of differing levels of activity on the financial results of a business
In any business, or, indeed, in life in general, hindsight is a beautiful thing. If only we could look into a crystal ball and find out exactly how many customers were going to buy our product, we would be able to make perfect business decisions and maximise profits.
Take a restaurant, for example. If the owners knew exactly how many customers would come in each evening and the number and type of meals that they would order, they could ensure that staffing levels were exactly accurate and no waste occurred in the kitchen. The reality is, of course, that decisions such as staffing and food purchases have to be made on the basis of estimates, with these estimates being based on past experience.
While management accounting information can’t really help much with the crystal ball, it can be of use in providing the answers to questions about the consequences of different courses of action. One of the most important decisions that need to be made before any business even starts is ‘how much do we need to sell in order to break-even?’ By ‘break-even’ we mean simply covering all our costs without making a profit.
This type of analysis is known as ‘cost-volume-profit analysis’ (CVP analysis) and the purpose of this article is to cover some of the straight forward calculations and graphs required for this part of the Performance Management syllabus, while also considering the assumptions which underlie any such analysis.
The objective of CVP analysis
CVP analysis looks primarily at the effects of differing levels of activity on the financial results of a business. The reason for the particular focus on sales volume is because, in the short-run, sales price, and the cost of materials and labour, are usually known with a degree of accuracy. Sales volume, however, is not usually so predictable and therefore, in the short-run, profitability often hinges upon it. For example, Company A may know that the sales price for product X in a particular year is going to be in the region of $50 and its variable costs are approximately $30.
It can, therefore, say with some degree of certainty that the contribution per unit (sales price less variable costs) is $20. Company A may also have fixed costs of $200,000 per annum, which again, are fairly easy to predict. However, when we ask the question, ‘Will the company make a profit in that year?’ the answer is ‘We don’t know’. We don’t know because we don’t know the sales volume for the year. However, we can work out how many sales the business needs to achieve in order to make a profit and this is where CVP analysis begins.
Methods for calculating the break-even point
The break-even point is when total revenues and total costs are equal, that is, there is no profit but also no loss made. There are three methods for ascertaining this break-even point:
(1) The equation method
A little bit of simple maths can help us answer numerous different cost‑volume-profit questions.
We know that total revenues are found by multiplying unit selling price (USP) by quantity sold (Q). Also, total costs are made up firstly of total fixed costs (FC) and secondly by variable costs (VC). Total variable costs are found by multiplying unit variable cost (UVC) by total quantity (Q). Any excess of total revenue over total costs will give rise to profit (P). By putting this information into a simple equation, we come up with a method of answering CVP type questions. This is done below continuing with the example of Company A above.
Total revenue – total variable costs – total fixed costs = Profit
(USP x Q) – (UVC x Q) – FC = P
(50Q) – (30Q) – 200,000 = P
Note: total fixed costs are used rather than unit fixed costs since unit fixed costs will vary depending on the level of output.
It would, therefore, be inappropriate to use a unit fixed cost since this would vary depending on output. Sales price and variable costs, on the other hand, are assumed to remain constant for all levels of output in the short-run, and, therefore, unit costs are appropriate.
Continuing with our equation, we now set P to zero in order to find out how many items we need to sell in order to make no profit, i.e. to break even:
(50Q) – (30Q) – 200,000 = 0
20Q – 200,000 = 0
20Q = 200,000
Q = 10,000 units.
The equation has given us our answer. If Company A sells less than 10,000 units, it will make a loss. If it sells exactly 10,000 units it will break-even, and if it sells more than 10,000 units, it will make a profit.
(2) The contribution margin method
This second approach uses a little bit of algebra to rewrite our equation above, concentrating on the use of the ‘contribution margin’. The contribution margin is equal to total revenue less total variable costs. Alternatively, the unit contribution margin (UCM) is the unit selling price (USP) less the unit variable cost (UVC). Hence, the formula from our mathematical method above is manipulated in the following way:
(USP x Q) – (UVC x Q) – FC = P
(USP – UVC) x Q = FC + P
UCM x Q = FC + P
Q = FC + P
UCM
So, if P = 0 (because we want to find the break-even point), then we would simply take our fixed costs and divide them by our unit contribution margin. We often see the unit contribution margin referred to as the ‘contribution per unit’.
Applying this approach to Company A again:
UCM = 20, FC = 200,000 and P = 0.
Q = FC
UCM
Q = 200,000
20
Therefore, Q = 10,000 units
The contribution margin method uses a little bit of algebra to rewrite our equation above, concentrating on the use of the ‘contribution margin’.
(3) The graphical method
With the graphical method, the total costs and total revenue lines are plotted on a graph; $ is shown on the y axis and units are shown on the x axis. The point where the total cost and revenue lines intersect is the break-even point. The amount of profit or loss at different output levels is represented by the distance between the total cost and total revenue lines. Figure 1 shows a typical break-even chart for Company A. The gap between the fixed costs and the total costs line represents variable costs.
Alternatively, a contribution graph could be drawn. While this is not specifically covered by the Performance Management syllabus, it is still useful to see it. This is very similar to a break-even chart; the only difference being that instead of showing a fixed cost line, a variable cost line is shown instead.
Hence, it is the difference between the variable cost line and the total cost line that represents fixed costs. The advantage of this is that it emphasises contribution as it is represented by the gap between the total revenue and the variable cost lines. This is shown for Company A in Figure 2.
Finally, a profit–volume graph could be drawn, which emphasises the impact of volume changes on profit (Figure 3). This is key to the Performance Management syllabus and is discussed in more detail later in this article.
Ascertaining the sales volume required to achieve a target profit
As well as ascertaining the break-even point, there are other routine calculations that it is just as important to understand. For example, a business may want to know how many items it must sell in order to attain a target profit.
Example 1
Company A wants to achieve a target profit of $300,000. The sales volume necessary in order to achieve this profit can be ascertained using any of the three methods outlined above. If the equation method is used, the profit of $300,000 is put into the equation rather than the profit of $0:
(50Q) – (30Q) – 200,000 = 300,000
20Q – 200,000 = 300,000
20Q = 500,000
Q = 25,000 units.
Alternatively, the contribution method can be used:
UCM = 20, FC = 200,000 and P = 300,000.
Q = FC + P
UCM
Q = 200,000 + 300,000
20
Therefore, Q = 25,000 units.
Finally, the answer can be read from the graph, although this method becomes clumsier than the previous two. The profit will be $300,000 where the gap between the total revenue and total cost line is $300,000, since the gap represents profit (after the break-even point) or loss (before the break-even point.)
A contribution graph shows the difference between the variable cost line and the total cost line that represents fixed costs. An advantage of this is that it emphasises contribution as it is represented by the gap between the total revenue and variable cost lines.
This is not a quick enough method to use in an exam so it is not recommended.
Margin of safety
The margin of safety indicates by how much sales can decrease before a loss occurs – ie it is the excess of budgeted revenues over break-even revenues. Using Company A as an example, let’s assume that budgeted sales are 20,000 units. The margin of safety can be found, in units, as follows:
Budgeted sales – break-even sales = 20,000 – 10,000 = 10,000 units.
Alternatively, as is often the case, it may be calculated as a percentage:
(Budgeted sales – break-even sales)/budgeted sales
In Company A’s case, it will be (10,000/20,000) x 100 = 50%.
Finally, it could be calculated in terms of $ sales revenue as follows:
(Budgeted sales – break-even sales) x selling price = 10,000 x $50 = $500,000.
Contribution to sales ratio
It is often useful in single product situations, and essential in multi‑product situations, to ascertain how much each $ sold actually contributes towards the fixed costs. This calculation is known as the contribution to sales or C/S ratio. It is found in single product situations by either simply dividing the total contribution by the total sales revenue, or by dividing the unit contribution margin (otherwise known as contribution per unit) by the selling price:
For Company A: ($20/$50) = 0.4
In multi-product situations, a weighted average C/S ratio is calculated by using the formula:
Total contribution/total sales revenue
This weighted average C/S ratio can then be used to find CVP information such as break-even point, margin of safety, etc.
Example 2
As well as producing product X described above, Company A also begins producing product Y. The following information is available for both products:

The weighted average C/S ratio of 0.34375 or 34.375% has been calculated by calculating the total contribution earned across both products and dividing that by the total revenue earned across both products.
The C/S ratio is useful in its own right as it tells us what percentage each $ of sales revenue contributes towards fixed costs; it is also invaluable in helping us to quickly calculate the break-even point in $ sales revenue, or the sales revenue required to generate a target profit. The break-even point in sales revenue can now be calculated this way for Company A:
Fixed costs/contribution to sales ratio = $200,000/0.34375 = $581,819 of sales revenue.
To achieve a target profit of $300,000:
(Fixed costs + required profit)/contribution to sales ratio = ($200,000 + $300,000)/0.34375 = $1,454,546.
Of course, such calculations provide only estimated information because they assume that products X and Y are sold in a constant mix of 2X to 1Y. In reality, this constant mix is unlikely to exist and, at times, more Y may be sold than X. Such changes in the mix throughout a period, even if the overall mix for the period is 2:1, will lead to the actual break-even point being different than anticipated. This point is touched upon again later in this article.
Contribution to sales ratio is often useful in single product situations, and essential in multi‑product situations, to ascertain how much each $ sold actually contributes towards the fixed costs.
Multi-product profit–volume charts
When discussing graphical methods for establishing the break-even point, we considered break-even charts and contribution graphs. These could also be drawn for a company selling multiple products, such as Company A in our example.
The one type of graph that hasn’t yet been discussed is a profit–volume graph. This is slightly different from the others in that it focuses purely on showing a profit/loss line and doesn’t separately show the cost and revenue lines. In a multi‑product environment, it is common to actually show two lines on the graph: one straight line, where a constant mix between the products is assumed; and one bow-shaped line, where it is assumed that the company sells its most profitable product first and then its next most profitable product, and so on.
In order to draw the graph, it is therefore necessary to work out the C/S ratio of each product being sold before ranking the products in order of profitability. It is easy here for Company A, since only two products are being produced, and so it is useful to draw a quick table as see on the spreadsheet below (prevents mistakes in the exam hall) in order to ascertain each of the points that need to be plotted on the graph in order to show the profit/loss lines.
The table should show the cumulative revenue, the contribution earned from each product and the cumulative profit/(loss). It is the cumulative figures which are needed to draw the graph.
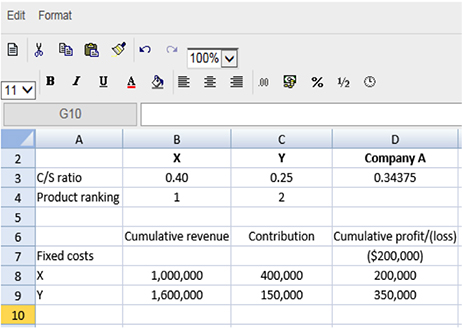
The graph can then be drawn (Figure 3), showing cumulative sales on the x axis and cumulative profit/loss on the y axis. It can be observed from the graph that, when the company sells its most profitable product first (X) it breaks even earlier than when it sells products in a constant mix. The break-even point is the point where each line cuts the x axis.
Limitations of cost-volume profit analysis
- Cost-volume-profit analysis is invaluable in demonstrating the effect on an organisation that changes in volume (in particular), costs and selling prices, have on profit. However, its use is limited because it is based on the following assumptions: Either a single product is being sold or, if there are multiple products, these are sold in a constant mix. We have considered this above in Figure 3 and seen that if the constant mix assumption changes, so does the break-even point.
- All other variables, apart from volume, remain constant – ie volume is the only factor that causes revenues and costs to change. In reality, this assumption may not hold true as, for example, economies of scale may be achieved as volumes increase. Similarly, if there is a change in sales mix, revenues will change. Furthermore, it is often found that if sales volumes are to increase, sales price must fall. These are only a few reasons why the assumption may not hold true; there are many others.
- The total cost and total revenue functions are linear. This is only likely to hold a short-run, restricted level of activity.
- Costs can be divided into a component that is fixed and a component that is variable. In reality, some costs may be semi-fixed, such as telephone charges, whereby there may be a fixed monthly rental charge and a variable charge for calls made.
- Fixed costs remain constant over the 'relevant range' - levels in activity in which the business has experience and can therefore perform a degree of accurate analysis. It will either have operated at those activity levels before or studied them carefully so that it can, for example, make accurate predictions of fixed costs in that range.
- Profits are calculated on a variable cost basis or, if absorption costing is used, it is assumed that production volumes are equal to sales volumes.
Written by a member of the Performance Management examining team


