Project appraisal 1 – pure equity finance
So now we have two ways of estimating the cost of equity (the return required by shareholders). Can this measurement of a company’s cost of equity be used as the discount rate with which to appraise capital investments? Yes it can, but only if certain conditions are met:
- A new investment can be appraised using the cost of equity only if equity alone is being used to fund the new investment. If a mix of funds is being used to fund a new investment, then the investment should be appraised using the cost of the mix of funds, not just the cost of equity.
- The gearing does not change. If the gearing changes, the cost of equity will change and its current value would no longer be applicable.
- The nature of the business is unchanged. The new project must be ‘more of the same’ so that the risk arising from business activities is unchanged. If the business risk did change, once again the old cost of equity would no longer be applicable.
These conditions are very restrictive and would apply only when an all-equity company issued more equity to do more of the same type of activity. Our approach needs to be developed if we are going to be able to appraise projects in more general environments.
In particular, we have to be able to deal with more general sources of finance, not just pure equity, and it would also be good if we could deal with projects which have different risk characteristics from existing activities.
Project appraisal 2 – same business activities, a mix of funds and constant gearing
Let us look at appraising a project which uses a mix of funds, but where those funds are raised so as to maintain the company’s gearing ratio. Remember, where there is a mix of funds, the funds are regarded as going into a pool of finance and a project is appraised with reference to the cost of that pool of finance. That cost is the weighted average cost of capital (WACC). As a preliminary to this discussion, we need briefly to revise how gearing can affect the various costs of capital, particularly the WACC. The three possibilities are set out in Example 1.
Example 1
ke = cost of equity; kd = pre-tax cost of debt; Vd = market value debt; Ve = market value equity. T is the tax rate.
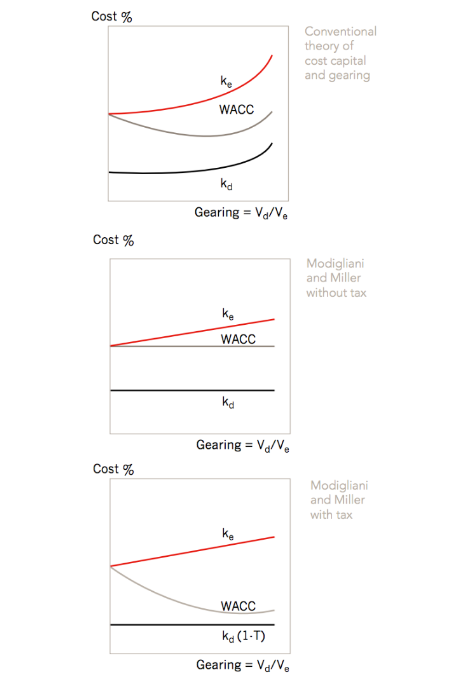
All three versions show that the cost of debt (Kd) is lower than the cost of equity (Ke). This is because debt is inherently less risky than equity (debt has constant interest; interest is paid before dividends; debt is often secured on assets; on liquidation creditors are repaid before equity shareholders). In the third version, cost of debt is further reduced because in an environment with corporation tax, interest payments enjoy tax relief.
Looking at the three cases in a little more detail:
Conventional theory
When there is only equity, the WACC starts at the cost of equity. As the more expensive equity finance is replaced by cheaper debt finance, the WACC decreases. However, as gearing increases further, both debt holders and equity shareholders will perceive more risk, and their required returns both increase. Inevitably, WACC must increase at some point. This theory predicts that there is an optimum gearing ratio at which WACC is minimised.
Modigliani and Miller (M&M) without tax
M&M were able to demonstrate that as gearing increases, the increase in the cost of equity precisely offsets the effect of more cheap debt so that the WACC remains constant.
Modigliani and Miller (M&M) with tax
Debt, because of tax relief on interest, becomes unassailably cheap as a source of finance. It becomes so cheap that even though the cost of equity increases, the balance of the effects is to keep reducing the WACC.
(Note: the M&M diagrams shown in Example 1 hold only for moderate levels of gearing. At very high levels of gearing, other costs come into play and the WACC can be shown to increase again – looking rather like the conventional theory.)
Whichever theory you believe, whether there is or isn’t tax, provided the gearing ratio does not change the WACC will not change. Therefore, if a new project consisting of more business activities of the same type is to be funded so as to maintain the present gearing ratio, the current WACC is the appropriate discount rate to use. In the special case of M&M without tax, you can do anything you like with the gearing ratio as the WACC will remain constant and will be equal to the ungeared cost of equity.
The condition that gearing is constant does not have to mean that upon every issue of capital both debt and equity also have to be issued. That would be very expensive in terms of transaction costs. What it means is that over the long term the gearing ratio will not change. That would certainly be the company’s ambition if it believed it was already at the optimum gearing ratio and minimum WACC. Therefore, this year, it might issue equity, the next debt and so on, so that the gearing and WACC hover around a constant position.
Project appraisal 3 - different business activities, a mix of funds and changing gearing
Let’s deal with different business activities first. Different activities will have different risk characteristics and hence any business carrying on those activities will have a different beta factor. The new funds being put into the new project are subject to the risk inherent in that project, and so should be discounted at a rate which reflects that risk. The formula:
E(ri) = Rf + ßi(E(rm) – Rf)
predicts the return that equity holders should require from a project with a given risk, as measured by the beta factor of that activity.
Note that we are doing something quite radical here: CAPM is allowing us to calculate a risk adjusted return on equity, tailor-made to fit the characteristics of the project being funded. All projects consist of capital being supplied, being invested and therefore being subject to risk, but the risk is determined by the nature of the project, not the company undertaking the project. The existing return on equity of the company that happens to be the vehicle for the project has become irrelevant.
We can extend this argument as follows. If the company doing the project is irrelevant there’s no reason why you can’t view the project as being undertaken by a new company specially set up for that project. The way the project is funded is the way the company is funded and, in particular, the appropriate discount rate to apply to the project is the WACC of the company/project, not its cost of equity – which would take into account only one component of the funding.
So we can calculate the cost of equity component which reflects project risk by using a beta value appropriate to that risk. The final steps are to adjust the cost of equity to reflect the gearing and then to calculate the appropriate discount rate, the WACC. The diagrams shown in Example 1 show (qualitatively) how the rates might move. No matter how reasonable the conventional theory seems, its big drawback is that it makes no quantitative predictions. However, the Modigliani and Miller theory does make quantitative predictions, and when combined with CAPM theory it allows the beta factor to be adjusted so that it takes into account not only business risk but also financial (gearing) risk. The formula you need is provided in the exam formula sheet:
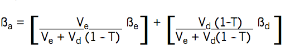
Where:
Ve = market value of equity;
Vd= market value of debt;
T = corporation tax rate;
ßa = the asset beta;
ße = the equity beta;
ßd = the debt beta.
ßd, the debt beta, is nearly always assumed to be zero, so the formula simplifies to:
ßa = Ve ße / Ve + Vd (1 – T)
What is meant by ßa (the asset beta), and ße (the equity beta)?
The asset beta is the beta (a measure of risk) which arises from the assets and the business the company is engaged in. No heed is paid to the gearing. An alternative name for the asset beta is the ‘ungeared beta’.
The equity beta is the beta which is relevant to the equity shareholders. It takes into account the business risk and the financial (gearing) risk because equity shareholders’ risk is affected by both business risk and financial (gearing) risk. An alternative name for the equity beta is the ‘geared beta’.
Note that the formula shows that if Vd = 0 (ie there is no debt), then the two betas are the same. If there is debt, the asset beta will always be less than the equity beta because the latter contains an additional component to account for gearing risk.
The formula is extremely useful as it allows us to predict the beta, and hence the cost of equity, for any level of gearing. Once you have the cost of equity, it is a straightforward process to calculate the WACC and hence discount the project.
To illustrate the use of CAPM in determining a discount rate, we will work through the following example, Example 2.
Example 2
Emway Co is a company engaged in road building. Its equity shares have a market value of $200 million and its 6% irredeemable bonds are valued at par, $50m. The company’s beta value is 1.3. Its cost of equity is 21.1%. (Note: this figure is quite high in the current economic situation and is used for illustration purposes. Currently, in a real situation, the cost of equity would be lower.)
The company is worried about the recession and is considering diversifying into supermarkets. It has investigated listed supermarkets and found one, Foodoo Co, which quite closely matches its plans. Foodoo has a beta of 0.9 and the ratio of the market value of its equity to its debt is 7:5. Emway plans that its new venture would be financed with a market value of equity to market value of debt ratio of 1:1.
The corporation tax rate is 20%. The risk free rate is 5.5%. The market return is 17.5%.
What discount rate should be used for the evaluation of the new venture?
Solution:
We have information supplied about a company in the right business but with the wrong gearing for our purposes. To adjust for the gearing we plan to have, we must always go through a theoretical ungeared company in the same business.
Again the beta supplied to us will be the beta measured in the market, so it will be an equity (geared) beta. Were Foodoo to be ungeared, its asset beta would be given by:
ßa = Ve ße / Ve + Vd (1 – T)
= (7 x 0.9)/(7 + 5 (1 – 0.2))
= 0.5727
This asset beta (ungeared beta) can now be adjusted to reflect the gearing ratio planned in the new venture:
0.5727 =1/(1 + 1(1 – 0.2))ße
So the planned ße will be 0.5727 x 1.8 = 1.03
Check that this makes sense. Foodoo has a gearing ratio of 7:5, equity to debt, a current beta of 0.9, and a cost of equity of 16.30 (calculated from CAPM as 5.5 + 0.9(17.5 – 5.5)). Were Foodoo ungeared, its beta would be 0.5727, and its cost of equity would be 12.37 (calculated from CAPM as 5.5 + 0.5727(17.5 - 5.5)).
Emway is planning a supermarket with a gearing ratio of 1:1. This is higher gearing, so the equity beta must be higher than Foodoo’s 0.9.
To calculate the return required by the suppliers of equity to the new project:
Required return = Risk free rate + ß (Return from market – Risk free rate)
= 5.5 + 1.03 (17.5 – 5.5) = 17.86%
17.86 is the return required by equity holders, but the new venture is being financed by a mix of debt and equity, and we need to calculate the cost of capital of this pool of finance.
Note that while Financial Management does not require students to undertake calculations of a project-specific WACC, they are required to understand it from a theoretical perspective.
The appropriate rate at which to evaluate the project is the WACC of the finance. Again, in the exam formula sheet you will find a formula for WACC consisting of equity and irredeemable debt.
Ke = 17.86%
Kd = 6% (from the cost of the debentures already issued by Emway)
WACC = 1/(1+1) x 17.86 + 1/(1+1) x 6 (1 – 0.2) = 11.33%
In terms of the diagram used in Example 1, for Modigliani and Miller with tax, what we have done for Foodoo’s figures is set out below. We started with information relating to a supermarket with a gearing ratio of debt:equity of 5:7, and an implied cost of equity of 16.30%. We strip out the gearing effect to arrive at an ungeared cost of equity of 12.37, then we project this forward to whatever level of gearing we want. In this example, this is a gearing ratio of 1:1 and this implies a cost of equity of 17.86%.
Finally, we take account of the cheap debt finance that is mixed with this equity finance, by calculating the WACC of 11.33%. This is the rate which should be used to evaluate the new supermarket project, funded by debt:equity of 1:1.
Ken Garrett is a freelance author and lecturer


