Relevant to ACCA Qualification Paper P4
Recent turmoil in the global credit market has dramatically underlined the importance of debt finance for both individuals and companies. For financial managers, it is just as important to understand how the debt market works, and how to cost debt capital, as it is to understand the operation of the much smaller equity market. This article explores the ways in which lenders decide the rate they will charge against any particular loan.
With equity, capital asset pricing theory teaches us that a firm’s exposure to market risk is the principal determinant of a firm’s equity cost of capital. With debt, market risk is not so important – what is important is whether a borrower will default on a loan. This is called ‘credit risk’.
Default occurs when the value of a borrower’s assets falls below the value of their outstanding debt. Therefore, two variables influence the potential loss to the lender: the chance of default occurring, and the part of the debt that can then be recovered by the sale of the firm’s assets.
At the simplest level, if the probability of a company defaulting is 5%, and only 80% of the debt can be recovered by the lender (that is, 20% will be lost), then at least an extra 1% (20% x 5%) will be charged to cover the potential loss. It’s not as simple as this in practice because the lender loses not only part of the sum advanced but also the accrued interest.
Lenders, whether in the form of banks or subscribers to bond issues, need to discover the potential loss faced on default and therefore the charge needed to cover exposure to credit risk. Lenders rarely undertake assessments of credit risk directly but normally employ the services of credit assessment agencies. For loans to the retail market, there are many credit agencies to which a lender can go. For bigger corporate loans, a lender may undertake the assessment itself or engage a credit rating agency to do it on its behalf. For the largest loans, or where the borrower is considering a bond issue, then the firm concerned will need to obtain a credit risk assessment from a rating agency such as Moody’s, Standard and Poor’s, or Fitch.
TWO APPROACHES TO CREDIT RISK ASSESSMENT
There are two methodologies for undertaking credit risk assessment. The first involves collecting financial and other measures and combining them into a multivariate scoring system. The earliest work on assessing bankruptcy risk was undertaken by William Beaver in 1966, who identified which of the common accounting ratios had the highest predictive value in assessing bankruptcy risk. He showed that one ratio – operating cash flow over total outstanding debt – successfully predicted default within five years with better than 70% accuracy. Edward Altman in the US, and Richard Taffler in the UK, developed more sophisticated multivariate models. Other models, such as that developed by Robert Kaplan and Gabriel Urwitz, focus on explaining the credit ratings given by the agencies. However, a common criticism of all these models is that they have weak theoretical support; they represent a form of brutal empiricism where data is dredged until measures emerge which best explain the phenomenon of interest.
Of course, over the decades, rating agencies have become more sophisticated in the methods they employ. They have also benefited from the theoretical developments that have led to the second of the two approaches to credit risk assessment. This approach is based on what are called ‘structural models’. Structural models rely on an assessment of the underlying riskiness of a firm’s assets or its cash generation, and the likelihood the firm will not be able to pay interest or repay capital on the due date.
ESTIMATING THE CREDIT PREMIUM FOR THE RISK-NEUTRAL LENDER
To take a simple example, supposing a firm has assets with a current value of $1m and outstanding debt of $0.4m. The volatility of those assets (as given by the standard deviation of monthly asset values) is 10%. From this volatility measure, we can calculate the likelihood that within the next 12 months those assets will fall in value to less than $0.4m, thereby triggering default.
A 10% monthly (σm) volatility can be converted to an annual volatility (σa) as follows:
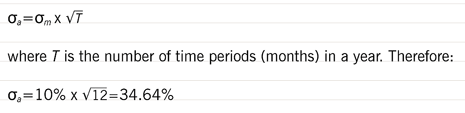
which, when applied to an average asset value of $1m, gives a standard deviation of $346,400. It is important to remember, when combining standard deviations, that they expand with the square root of time.
In this example, the ‘distance to default’ in value terms is $1m less $0.4m, or $0.6m. Dividing this by the standard deviation tells us the number of standard deviations (z) below the average asset value the default level lies.
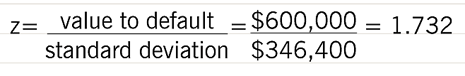
Using standard normal distribution tables (or the =normsdist() function in Excel) we can show that the proportion represented by 1.732 standard deviations is 0.4584. Adding this to the probability of an asset value being above the mean (0.5) gives a total probability of not defaulting of 0.9548 or, conversely, a probability of defaulting of 0.0452.
The second part of the default assessment is to estimate the potential ‘recoverability’ of the debt. A number of issues influence recoverability such as the nature of the firm’s assets and their saleability, any covenants which impose restrictions on their disposal, the priority of the lender, and any directors’ guarantees that may be in place. From this it is easy to see why banks often proceed with unseemly haste when they foreclose. For a bank, at that point, the priority is to protect the recoverability of the assets which support its loan.
Using some simple data we can then work towards an estimate of the ‘default spread’ that a bank will charge for a loan. Assume it assesses the recoverability of the debt as 80% and that it, in turn, pays LIBOR of 5% to raise finance on the financial market. On a loan of $400,000, the bank would expect to receive LIBOR plus the premium it wishes to charge at the end of the year, giving an overall rate of i %. A simple decision tree shows how the bank equates the present value certain sum of $400,000 to the uncertain future outcomes on the loan:
From the tree we can see that there are two possible outcomes. Either the lender receives its principal sum back, plus interest at i%, or it receives just 80% of that value. We have discounted at LIBOR on the assumption that the lender is neutral towards risk – an assumption we will relax in just a moment. We can express this decision tree as a simple equation:
or the percentage rate is 5.96%, which is 96 basis points over LIBOR.
ADJUSTING THE RATE FOR RISK AVERSION
Banks, however, are not neutral towards risk. The potential loss of 20% of the loan is more significant to them than the potential gain if the lender remains solvent. To compensate, a bank will add a percentage to the discount rate to cover its aversion to risk, and any other charges it may wish to make. If we assume, in this case, that the lender requires an additional 50 basis points (0.5%) then the previous calculation becomes:
INSERT FIG 4
$400,000=0.9548 x + 0.0452 x rearranging i = -1=0.0646
which gives a rate of 6.46%.
A problem with this type of analysis is how to estimate the asset value of the firm and the volatility of that asset value. The solution comes from the theory of options. A call option is an option on the part of the holder to purchase an asset at a set price on or before a set date. In a limited liability company partly financed by debt, equity investors can ‘walk away’ in the event that the value of the firm’s assets is less than the amount borrowed. Alternatively, if there is surplus asset value they have the option to redeem the debt and take the difference. The value of the firm’s equity is therefore the value of a call option written by the lender on the underlying assets of the business.
In option pricing terms, the value of the debt is the exercise price, the value of the assets is the value of the underlying, and the time to exercise is the term to maturity on the debt. All we need to complete the inputs to the Black Scholes Option Pricing Model is the volatility of the assets and the risk-free rate. All we can directly observe in practice is the value of the firm’s equity (which is the value of the call option on the firm’s assets). What we cannot observe directly is the value of those assets and their volatility. However, it is a straightforward extension of the Black Scholes Model to find the asset value and volatility to give a stated equity value. How this is done will be the subject of a future article.
CONCLUSION
The issue of how much a firm will have to pay for its debt finance is important for the financial manager; they need to know what the likely cost of debt capital will be for a given financing package before entering into discussion with lenders, or before setting the coupon rate on a debt issue. Lenders need to know, in their turn, the amount above LIBOR that they should charge to cover the loss on default and as compensation for the risk involved.
As with much in finance, the calculations are straightforward – the difficulty is in identifying the values to go into the formulae. However, by working through the simple example above we can gain an insight into those factors that influence a bank when setting the rate for a loan, and this knowledge is an important tool in the hands of the financial manager.
REFERENCES
Written by a member of the Paper P4 examining team