Relevant to ACCA Qualification Paper P4
Internal rate of return (IRR) has never had a good academic press. Compared with net present value (NPV), IRR has many drawbacks: it is only a relative measure of value creation, it can have multiple answers, it’s difficult to calculate, and it appears to make a reinvestment assumption that is unrealistic. But financial managers like it. IRR expresses itself as a percentage measure of project performance; it also provides a useful tool to measure ‘headroom’ when negotiating with suppliers of funds. The question we will try to answer is whether there is an even better measure which keeps the benefits of IRR without the drawbacks.
IRR is the discount rate which delivers a zero NPV on a given project. Discounting, like compounding cash flows, assumes that not only the initial investment, but also the net cash produced by a project, is reinvested within the project as it proceeds. Thus, the IRR is also the investment/reinvestment rate which a project generates over its lifetime – and hence IRR is also known as the ‘economic yield’ on an investment.
MODIFIED INTERNAL RATE OF RETURN
Modified internal rate of return (MIRR) is a similar technique to IRR. Technically, MIRR is the IRR for a project with an identical level of investment and NPV to that being considered but with a single terminal payment. A simple example will help explain matters.
EXAMPLE 1
A project entails an initial investment of $1,000, and offers cash returns of $400, $500, and $300 at the end of years one, two and three respectively. The company’s cost of capital is 10%.
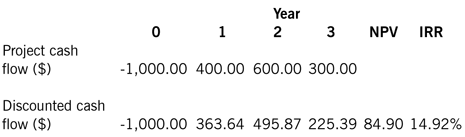
The table shows the discounted cash flow, the NPV of the project, and its IRR. The project is viable in NPV terms, and notice also that this is reflected in the IRR which is greater than the firm’s cost of capital of 10%.
There are four methods we can use to determine the MIRR, two using a spreadsheet package, and two manual methods – which are more relevant to the exam.
Method 1 – spreadsheet package
This is a useful method to start with as it will allow you to familiarise yourself with the definition of MIRR. To do this, convert the year one and year two cash flow to zero, put a specimen value (say $1,500) in year three, and then calculate the NPV:

Note that the NPV is higher. Using the ‘goal seek’ function in Excel (under ‘data>what-if’ in the 2007 version, or under ‘tools’ in the 2003 version), find the value of the year three cash flow which gives an NPV of $84.90. The result is:
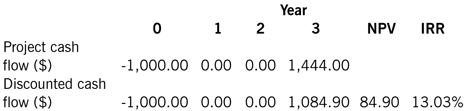
Notice that the IRR is now 13.03% compared with the 14.92% originally calculated, and this is the MIRR for this project.
Method 2 – spreadsheet package
In Excel and other spreadsheet software you will find an MIRR function of the form: =MIRR(value_range,finance_rate,reinvestment_rate) where the finance rate is the firm’s cost of capital and the reinvestment is any chosen rate – in our case we will use 10%.
=MIRR (value_range,10%,10%)
Using this function on the original project cash flows gives 13.03%. You can then experiment to see what happens if you vary the reinvestment rate. For example, if you put in the original IRR of 14.92%, you will also get an MIRR of 14.92%.
=MIRR(value_range,10%,14.92%)
Method 3 – calculator
Now you have learnt how to perform the calculations on a computer, we also look at two approaches to MIRR calculations – by hand and with a calculator.
The traditionally taught calculator method is laborious and easy to get wrong. We will therefore proceed in two stages.
Stage 1: Taking the project cash flows from the return phase (ie year one forward in this case), compound each cash flow forward to the end of the project using the firm’s cost of capital.
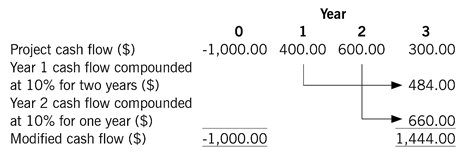
Note, as with the first spreadsheet method we have a modified cash flow which has an identical NPV to the original project.
Stage 2: Taking the total of the cash flows extended to year three, calculate the discount rate required to set this value when discounted equal to the outlay. To do this we need to use the following formula:

The only problem with this method is that it is time consuming to perform for anything but the smallest project.
Method 4 – manual spreadsheet
This method is much more straightforward and employs a simple formula which is quick and easy to apply:
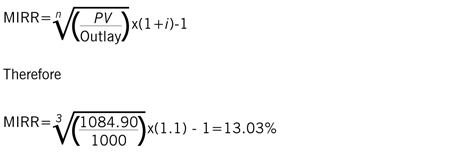
Take the present value (PV) of the project cash flows from the recovery phase (note not the NPV), divide by the outlay and take the ‘ n th’ root of the result. Multiply the result by one plus the cost of capital (1.1 in this case), deduct one and you have the answer.
MORE COMPLEX CAPITAL INVESTMENT PROJECTS
Not all projects promise cash flows of the simple type outlined above. The most common difficulty is where the investment phase stretches over a number of years. To handle this type of problem we divide the cash flows from the project into an ‘investment’ phase and a ‘return’ phase. For example, assume that a project has an investment phase over 12 months which consists of an initial investment of $700 and a further investment of $300, 12 months later. At the end of the second year, the project is expected to commence the return phase with a cash return of $400, followed by $600 and $300 in years three and four respectively. As before, we will assume a 10% cost of capital as the discount rate.
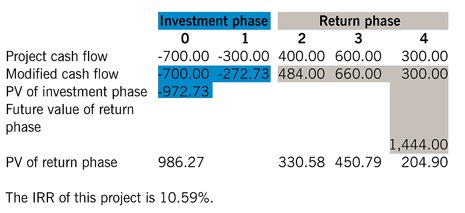
Investment phase Return phase 0 1 2 3 4 Project cash flow -700.00 -300.00 400.00 600.00 300.00 Modified cash flow -700.00 -272.73 484.00 660.00 300.00 PV of investment phase -972.73 Future value of return phase 1,444.00 PV of return phase 986.27 330.58 450.79 204.90 The IRR of this project is 10.59%.
Using method 1, the modified cash flow is calculated by discounting the investment phase at 10% to give a PV of capital investment of $972.73; compounding the return phase to a terminal cash flow gives $1,444.00. The MIRR is calculated as follows, but this time for a four-year project.

CONCLUSION
Using the formula, MIRR is quicker to calculate than IRR. MIRR is invariably lower than IRR and some would argue that it makes a more realistic assumption about the reinvestment rate. However, there is much confusion about what the reinvestment rate implies.
Both the NPV and the IRR techniques assume the cash flows generated by a project are reinvested within the project. This is not always the case; as many books suggest, they are often reinvested elsewhere within the firm and it is not a necessary assumption that the firm is capable of generating that IRR on its other business. Indeed, one implication of the MIRR is that the project is not capable of generating cash flows as predicted and that the project’s NPV is overstated. The only significant advantages of the MIRR technique are that it is relatively quicker to calculate and does not give the multiple answers that can sometimes arise with the conventional IRR. That may be a very small gain compared with the loss of financial significance that the MIRR implies.
REFERENCE
Ryan R, Corporate Finance and Valuation, Thomson Learning, London, 2006.
Written by a member of the Paper P4 examining team


